题目内容
圆C:x2+y2-x+2y=0的圆心是 ,与圆C关于直线l:x-y+1=0对称的圆的方程是 .
考点:关于点、直线对称的圆的方程,圆的标准方程
专题:计算题,直线与圆
分析:先求出圆x2+y2-x+2y=0的圆心和半径;再利用两点关于已知直线对称所具有的结论,求出所求圆的圆心坐标即可求出结论.
解答:
解:∵圆x2+y2-x+2y=0转化为标准方程为(x-
)2+(y+1)2=
,
所以其圆心为:C(
,-1),r=
设(
,-1)关于直线x-y+1=0对称点为:(a,b)
则有
,∴a=-2,b=1.5
故所求圆的圆心为:(-2,1.5),半径为
.
所以所求圆的方程为:(x+2)2+(y-1.5)2=
.
故答案为:(
,-1),(x+2)2+(y-1.5)2=
.
| 1 |
| 2 |
| 5 |
| 4 |
所以其圆心为:C(
| 1 |
| 2 |
| ||
| 2 |
设(
| 1 |
| 2 |
则有
|
故所求圆的圆心为:(-2,1.5),半径为
| ||
| 2 |
所以所求圆的方程为:(x+2)2+(y-1.5)2=
| 5 |
| 4 |
故答案为:(
| 1 |
| 2 |
| 5 |
| 4 |
点评:本题主要考查圆的方程的求法.解决问题的关键在于会求点关于直线的对称点的坐标,主要利用两个结论:①两点的连线和已知直线垂直;②两点的中点在已知直线上.

练习册系列答案
相关题目
如图是一个几何体的三视图,若该几何体的体积为
,则主视图中三角形的高x的值为( )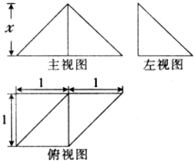
| 3 |
| 8 |

A、
| ||
B、
| ||
| C、1 | ||
D、
|
下列函数中,既是偶函数又在(0,+∞)上单调递减的函数是( )
| A、y=x3 | ||
| B、y=-x2+1 | ||
| C、y=|x|+1 | ||
D、y=
|
函数f(x)=
在[2,+∞)上( )
| 1 |
| x |
| A、有最大值无最小值 |
| B、有最小值无最大值 |
| C、有最大值和最小值 |
| D、无最大值和最小值 |
下列函数中周期为π且为偶函数的是( )
A、y=cos(2x-
| ||
B、y=sin(2x+
| ||
C、y=sin(x+
| ||
D、y=cos(x-
|