题目内容
在△ABC中，三个角满足2A=B+C，且最大边与最小边分别是方程3x2-27x+32=0的两根，则△ABC的外接圆面积是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：正弦定理
专题：解三角形
分析：根据2A=B+C求出A=60°，并判断出最大边与最小边，利用一元二次方程的根与系数的关系和题意，得出最大边与最小边之间的等量关系，再利用余弦定理求出边a，利用正弦定理求出外接圆的半径，再外接圆的面积即可．
解答：
解：由题意得，2A=B+C，则A=60°，所以a既不是最大边也不是最小边，
不妨假设c为最大边，b为最小边，则
，
由余弦定理得，a2=b2+c2-2bccos60°=（b+c）2-3bc=49，
解得a=7（a=-7舍去），
由正弦定理得，2R=
=
=
，则R=
，
所以△ABC的外接圆面积是S=πR2=
π，
故选：B．
不妨假设c为最大边，b为最小边，则
|
由余弦定理得，a2=b2+c2-2bccos60°=（b+c）2-3bc=49，
解得a=7（a=-7舍去），
由正弦定理得，2R=
| a |
| sinA |
| 7 |
| sin60° |
14
| ||
| 3 |
7
| ||
| 3 |
所以△ABC的外接圆面积是S=πR2=
| 49 |
| 3 |
故选：B．
点评：本题考查余弦、正弦定理，内角和定理的应用，以及一元二次方程根与系数的关系和三角形三边关系，综合性较强．
练习册系列答案
相关题目
已知数列{an}的首项a1=2，且an+1=2an+1，（n≥1，n∈N+），则a5=（ ）
| A、7 | B、15 | C、30 | D、47 |
知f（x）是实数集上的偶函数，且在区间[0，+∞）上是增函数，则f（-2），f（-π），f（3）的大小关系是（ ）
| A、f（-π）＞f（-2）＞f（3） |
| B、f（3）＞f（-π）＞f（-2） |
| C、f（-2）＞f（3）＞f（-π） |
| D、f（-π）＞f（3）＞f（-2） |
设l、m为两条直线，α为一个平面，下列四个命题中正确的是（ ）
| A、若l∥m，m?α，则l∥α |
| B、若l∥α，m?α，则l∥m |
| C、若l∥α，m?α，则l与m不平行 |
| D、若l∥m，l∥α，m?α，则m∥α |
观察下列各式：55=3125，56=15625，57=78125，58=390625，59=1953125则52012的末四位数字为（ ）
| A、3125 | B、5625 |
| C、0625 | D、8125 |
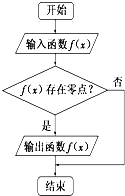执行如图所示的程序框图，若输入如下四个函数：