题目内容
8.在下列给出的命题中,所有正确命题的序号为①②.①函数y=2x3-3x+1的图象关于点(0,1)成中心对称;
②对?x,y∈R,若x+y≠0,则x≠1,或y≠-1;
③若实数x,y满足x2+y2=1,则$\frac{y}{x+2}$的最大值为$\sqrt{3}$;
④若△ABC为钝角三角形,∠C为钝角,则sinA>cosB.
分析 ①函数y=2x3-3x+1=的图象关于点(0,1)成中心对称,假设点(x0,y0)在函数图象上,则其关于①点(0,1)的对称点为(-x0,2-y0)也满足函数的解析式,则;
②对?x,y∈R,若x+y≠0,对应的是直线y=-x以外的点,则x≠1,或y≠-1;
③若实数x,y满足x2+y2=1,则$\frac{y}{x+2}$=$\frac{y-0}{x-(-2)}$,可以看作是圆x2+y2=1上的点与点(-2,0)连线的斜率,其最大值为$\frac{\sqrt{3}}{3}$;
④若△ABC为钝角三角形,若A、B∈(0,$\frac{π}{4}$)时,sinA<cosB,.
解答 解:①函数y=2x3-3x+1=的图象关于点(0,1)成中心对称,假设点(x0,y0)在函数图象上,则其关于①点(0,1)的对称点为(-x0,2-y0)也满足函数的解析式,则①正确;
②对?x,y∈R,若x+y≠0,对应的是直线y=-x以外的点,则x≠1,或y≠-1,②正确;
③若实数x,y满足x2+y2=1,则$\frac{y}{x+2}$=$\frac{y-0}{x-(-2)}$,可以看作是圆x2+y2=1上的点与点(-2,0)连线的斜率,其最大值为$\frac{\sqrt{3}}{3}$,③错误;
④若△ABC为钝角三角形,若A、B∈(0,$\frac{π}{4}$)时,sinA<cosB,④错误.
故答案为:①②
点评 本题考查了判断命题真假,函数的性质,属于中档题..

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 甲、乙两名同学在五次考试中的数学成绩统计用茎叶图表示如图所示,则甲、乙两名同学成绩稳定的是乙.
甲、乙两名同学在五次考试中的数学成绩统计用茎叶图表示如图所示,则甲、乙两名同学成绩稳定的是乙. 如图所示,五面体ABCDFE中,AB∥CD∥EF,四边形ABCD,ABEF,CDFE都是等腰梯形,并且平面ABCD⊥平面ABEF,AB=12,CD=3,EF=4,梯形ABCD的高为3,EF到平面ABCD的距离为6,则此五面体的体积为57.
如图所示,五面体ABCDFE中,AB∥CD∥EF,四边形ABCD,ABEF,CDFE都是等腰梯形,并且平面ABCD⊥平面ABEF,AB=12,CD=3,EF=4,梯形ABCD的高为3,EF到平面ABCD的距离为6,则此五面体的体积为57.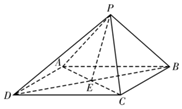 如图,四棱锥P-ABCD的底面ABCD是菱形,∠ADC=60°,PA=PC,PD⊥PB,AC∩BD=E,二面角P-AC-B的大小为60°.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠ADC=60°,PA=PC,PD⊥PB,AC∩BD=E,二面角P-AC-B的大小为60°.