题目内容

14．设x∈R，则“|x-2|＜1”是“x2+x-2＞0”的（　　）
A．既不充分也不必要条件B．充要条件
C．充分而不必要条件D．必要而不充分条件

分析 根据不等式的性质，结合充分条件和必要条件的定义进行判断即可．

解答 解：由“|x-2|＜1”得1＜x＜3，
由x2+x-2＞0得x＞1或x＜-2，
即“|x-2|＜1”是“x2+x-2＞0”的充分不必要条件，
故选：C．

点评 本题主要考查充分条件和必要条件的判断，比较基础．

练习册系列答案
相关题目
4．由曲线y=$\sqrt{x}$和直线x+y=2，y=-$\frac{1}{3}$x围成的图形的面积为$\frac{13}{6}$．
5．已知命题p：函数f（x）=lg（ax2-4x+a）的定义域为R；命题q：不等式2x2+x＞2+ax，对?x∈（-∞，-1）上恒成立．
（1）若命题p为真命题，求实数a的取值范围；
（2）若“p∨q”为真命题，命题“p∧q”为假命题，求实数a的取值范围．
2．圆（x-2）2+（y+1）2=4关于直线 y=x+1对称的圆的方程为（　　）
A．（x-2）2+（y-3）2=4B．（x+2）2+（y-3）2=4C．（x+2）2+（y+3）2=4D．（x-2）2+（y+3）2=4
9．设x，y满足$\left\{\begin{array}{l}{x≤y}\\{y≤10-2x}\\{x≥1}\end{array}\right.$，$\overrightarrow{a}$=（2x-y，m），$\overrightarrow{b}$=（-1，1）}${x≥1}\end{array}$，若$\overrightarrow{a}$∥$\overrightarrow{b}$，则m的最大值为6．
19．在等比数列{an}中，若a1=-1，a2+a3=-2，则其公比为-2或1．
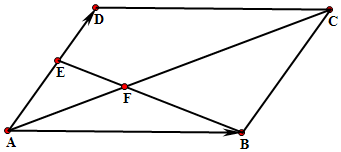6．如图，平行四边形ABCD中，点E在线段AD上，BE与AC交于点F，设$\overrightarrow{AB}=a，\overrightarrow{AD}=b$．
（I）若E为AD的中点，用向量$\overrightarrow{a}，\overrightarrow{b}$表示$\overrightarrow{CE}+\overrightarrow{BE}$；
（II）用向量的方法探究：在线段AD上是否存在点E，使得点F恰好为BE的一个三等分点，若有，求出满足条件的所有点E的位置；若没有，说明理由．
3．已知定义在R上的函数f（x）满足f（x+y）=f（x）+f（y）+4xy，f（1）=1，则f（-2）=（　　）
A．-2B．2C．6D．10
4．设实数m，n满足$\frac{6}{m}+\frac{4}{n}=\sqrt{2mn}$，则mn的最小值为4$\sqrt{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网