题目内容
9.设x,y满足$\left\{\begin{array}{l}{x≤y}\\{y≤10-2x}\\{x≥1}\end{array}\right.$,$\overrightarrow{a}$=(2x-y,m),$\overrightarrow{b}$=(-1,1)}${x≥1}\end{array}$,若$\overrightarrow{a}$∥$\overrightarrow{b}$,则m的最大值为6.分析 由$\overrightarrow{a}$∥$\overrightarrow{b}$,可得y=2x+m.画出可行域$\left\{\begin{array}{l}{x≤y}\\{y≤10-2x}\\{x≥1}\end{array}\right.$,可得直线y=2x+m经过点A时,m取得最大值.
解答 解:∵$\overrightarrow{a}$∥$\overrightarrow{b}$,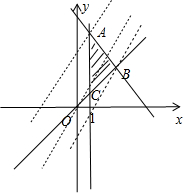
∴2x-y+m=0,即y=2x+m.
画出可行域$\left\{\begin{array}{l}{x≤y}\\{y≤10-2x}\\{x≥1}\end{array}\right.$,
联立$\left\{\begin{array}{l}{x=1}\\{y=10-2x}\end{array}\right.$,解得x=1,y=8.
∴A(1,8),
则直线y=2x+m经过点A时,m取得最大值.
m=8-2=6.
故答案为:6.
点评 本题考查线性规划的运用、直线斜率与截距的意义、向量共线定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
4.设全集U是实数集R,集合M={x|x2>2x},N=$\left\{{x|\frac{2-x}{x-1}≥0}\right\}$,则(∁UM)∩N为( )
| A. | {x|1<x<2} | B. | {x|1≤x≤2} | C. | {x|1<x≤2} | D. | {x|1≤x<2} |
14.设x∈R,则“|x-2|<1”是“x2+x-2>0”的( )
| A. | 既不充分也不必要条件 | B. | 充要条件 | ||
| C. | 充分而不必要条件 | D. | 必要而不充分条件 |
19.在△ABC中,a,b,c分别是角A,B,C所对边的边长,若cosC+sinC-$\frac{2}{cosB+sinB}$=0,则$\frac{a+b}{c}$的值是( )
| A. | $\sqrt{2}$-1 | B. | $\sqrt{2}$+1 | C. | $\sqrt{3}$+1 | D. | 2 |