题目内容
(1)求证:函数f(x)=2x+2-x在[0,+∞)上是单调递增函数;
(2)求函数f(x)=2x+2-x(x∈R)的值域;
(3)设函数h(x)=4x+4-x+a(2x+2-x)(a∈R),求h(x)的最小值φ(a).
(2)求函数f(x)=2x+2-x(x∈R)的值域;
(3)设函数h(x)=4x+4-x+a(2x+2-x)(a∈R),求h(x)的最小值φ(a).
考点:指数函数综合题
专题:综合题,函数的性质及应用
分析:(1)利用导数可证明单调性;
(2)先判断函数的奇偶性,由(1)可知函数在[1,+∞)上的单调性,由单调性及奇偶性可得值域;
(3)h(x)=(2x+2-x)2+a(2x+2-x)-2,令2x+2-x=t,则h(x)=m(t)=t2+at-2,t∈[2,+∞),按照对称轴与区间的位置分两种情况讨论可得;
(2)先判断函数的奇偶性,由(1)可知函数在[1,+∞)上的单调性,由单调性及奇偶性可得值域;
(3)h(x)=(2x+2-x)2+a(2x+2-x)-2,令2x+2-x=t,则h(x)=m(t)=t2+at-2,t∈[2,+∞),按照对称轴与区间的位置分两种情况讨论可得;
解答:
(1)证明:∵f(x)=2x+2-x,
∴f′(x)=2xln2-2-xln2=(2x-2-x)ln2=
•ln2,
∵x∈[0,+∞),∴f′(x)≥0,
∴f(x)=2x+2-x在[0,+∞)上是单调递增函数;
(2)解:∵f(-x)=2x+2-x=f(x),∴f(x)为R上的偶函数,
由(1)知f(x)在[0,+∞)上为增函数,则x≥0时f(x)≥20+20=2,
由偶函数性质知在(-∞,0]上f(x)≥2,
∴f(x)的值域为[2,+∞);
(3)解:∵h(x)=(2x+2-x)2+a(2x+2-x)-2,令2x+2-x=t,
则h(x)=m(t)=t2+at-2,t∈[2,+∞),
∵函数m(t)的对称轴方程为t=-
,
∴①当-
≥2,即a≤-4时,φ(a)=m(-
)=-
-2;
②当-
<2,即a>-4时,φ(a)=m(2)=2a+2;
综上所述,φ(a)=
.
∴f′(x)=2xln2-2-xln2=(2x-2-x)ln2=
| 22x-1 |
| 2x |
∵x∈[0,+∞),∴f′(x)≥0,
∴f(x)=2x+2-x在[0,+∞)上是单调递增函数;
(2)解:∵f(-x)=2x+2-x=f(x),∴f(x)为R上的偶函数,
由(1)知f(x)在[0,+∞)上为增函数,则x≥0时f(x)≥20+20=2,
由偶函数性质知在(-∞,0]上f(x)≥2,
∴f(x)的值域为[2,+∞);
(3)解:∵h(x)=(2x+2-x)2+a(2x+2-x)-2,令2x+2-x=t,
则h(x)=m(t)=t2+at-2,t∈[2,+∞),
∵函数m(t)的对称轴方程为t=-
| a |
| 2 |
∴①当-
| a |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
②当-
| a |
| 2 |
综上所述,φ(a)=
|
点评:该题考查指数函数与二次函数的综合,考查函数的单调性、奇偶性及其应用,考查学生解决问题的能力.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
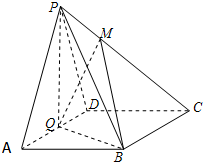 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,点M在线段PC上,MC=2PM.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,点M在线段PC上,MC=2PM. 已知一正整数的数阵如图所示(从上至下第1行是1,第2行是3、2,…),则数字2014是从上至下第
已知一正整数的数阵如图所示(从上至下第1行是1,第2行是3、2,…),则数字2014是从上至下第