题目内容
设{an}是由正数组成的数列,其前n项和为Sn,且满足关系:Sn=
(an-1)(an+3)
(1)求数列{an}的通项公式;
(2)求Tn=
+
+
+…+
.
| 1 |
| 4 |
(1)求数列{an}的通项公式;
(2)求Tn=
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| S3 |
| 1 |
| Sn |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由于Sn=
(an-1)(an+3),当n≥2时,Sn-1=
(an-1-1)(an-1+3),两式相减并整理得:(an+an-1)•(an-an-1-2)=0,利用等差数列的通项公式即可得出.
(2)利用等差数列的前n项和公式可得Sn,再利用“裂项求和”即可得出Tn.
| 1 |
| 4 |
| 1 |
| 4 |
(2)利用等差数列的前n项和公式可得Sn,再利用“裂项求和”即可得出Tn.
解答:
解:(1)∵Sn=
(an-1)(an+3),
∴当n≥2时,Sn-1=
(an-1-1)(an-1+3),
两式相减并整理得:(an+an-1)•(an-an-1-2)=0,
∴an>0,
∴an-an-1=2,
∴数列{an}成等差数列 公差d=2,
又当n=1时,∴a1=S1=
(a1-1)(a1+3),
解得a1=3.
∴an=3+2(n-1)=2n+1.
(2)由(1)可得Sn=
=n(n+2).
∴
=
=
(
-
).
∴Tn=
+
+
+…+
=
•(1+
-
-
)
=
-
.
| 1 |
| 4 |
∴当n≥2时,Sn-1=
| 1 |
| 4 |
两式相减并整理得:(an+an-1)•(an-an-1-2)=0,
∴an>0,
∴an-an-1=2,
∴数列{an}成等差数列 公差d=2,
又当n=1时,∴a1=S1=
| 1 |
| 4 |
解得a1=3.
∴an=3+2(n-1)=2n+1.
(2)由(1)可得Sn=
| n(3+2n+1) |
| 2 |
∴
| 1 |
| Sn |
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
∴Tn=
| 1 |
| 1•3 |
| 1 |
| 2•4 |
| 1 |
| 3•5 |
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=
| 3 |
| 4 |
| 2n+3 |
| 2(n+1)(n+2) |
点评:本题考查了递推式的应用、等差数列的通项公式及其前n项和公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设a、b∈z,且a≠0,则(a-b)a2<0,且a<b的( )条件.
| A、充分不必要 |
| B、必要而不充分 |
| C、充要 |
| D、既不充分也不必要 |
设f(x)与g(x)是定义在同一区间[m,n]上的两个函数,若函数y=f(x)-g(x)在x∈[m,n]上有两个不同的零点,则称f(x)和g(x)在[m,n]上是“相关函数”,区间[m,n]是“相关区间”.若f(x)=-x2+tx-3与g(x)=2x+t在[2,4]上是“相关函数”,则实数t的取值范围是( )
A、(4+2
| ||||
B、{4+2
| ||||
C、(-∞,4-2
| ||||
D、(4+2
|
直角坐标系中坐标原点O关于直线l:2xtanα+y-1=0的对称点为A(1,1),则tan2α的值为( )
A、-
| ||
B、
| ||
| C、1 | ||
D、
|
直线x+
y+3=0的倾斜角是( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
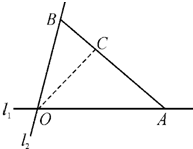 如图,在C城周边已有两条公路l1,l2在点O处交汇,且它们的夹角为75°.已知OC=(
如图,在C城周边已有两条公路l1,l2在点O处交汇,且它们的夹角为75°.已知OC=(