题目内容
已知向量
=(
sinx,-cosx),
=(cosx,cosx),记函数f(x)=
•
.
(1)求f(x)的最小正周期及单调递增区间;
(2)设△ABC的内角A,B,C的对边分别是a,b,c,且c=
,f(C)=
,若向量
=(1,sinA)与
=(2,sinB)共线,求a,b的值.
| a |
| 3 |
| b |
| a |
| b |
(1)求f(x)的最小正周期及单调递增区间;
(2)设△ABC的内角A,B,C的对边分别是a,b,c,且c=
| 3 |
| 1 |
| 2 |
| m |
| n |
考点:余弦定理,平面向量数量积的运算,两角和与差的正弦函数
专题:三角函数的图像与性质,解三角形
分析:(1)函数化简为:f(x)=sin(2x-
)-
,即可求得f(x)的最小正周期及单调递增区间;
(2)由f(C)=
可求C的值,根据向量m与n共线可求得b=2a,再根据a2+b2-ab=3,进而解得a,b的值.
| π |
| 6 |
| 1 |
| 2 |
(2)由f(C)=
| 1 |
| 2 |
解答:
解:(1)依题意,f(x)=
sinxcosx-cos2x=
sin2x-
=
sin2x-
cos2x-
=sin(2x-
)-
(3分)
所以最小正周期T=
=π,(4分)
令2kπ-
≤2x-
≤2kπ+
,k∈Z,解得kπ-
≤x≤kπ+
,k∈Z,
所以f(x)的单调递增区间是:[kπ-
,kπ+
],k∈Z.(6分)
(2)由f(C)=sin(2C-
)-
=
,得sin(2C-
)=1,(7分)
因为0<C<π,所以-
<2C-
<
,所以2C-
=
,解得C=
,(8分)
因为向量m=(1,sinA)与n=(2,sinB)共线,所以sinB=2sinA,由正弦定理得b=2a,…①(9分)
在△ABC中,由余弦定理得c2=a2+b2-2abcos
,即a2+b2-ab=3,…②(11分)
由①②,解得a=1,b=2.(13分)
| 3 |
| ||
| 2 |
| 1+cos2x |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
所以最小正周期T=
| 2π |
| 2 |
令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
所以f(x)的单调递增区间是:[kπ-
| π |
| 6 |
| π |
| 3 |
(2)由f(C)=sin(2C-
| π |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
因为0<C<π,所以-
| π |
| 6 |
| π |
| 6 |
| 11π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
因为向量m=(1,sinA)与n=(2,sinB)共线,所以sinB=2sinA,由正弦定理得b=2a,…①(9分)
在△ABC中,由余弦定理得c2=a2+b2-2abcos
| π |
| 3 |
由①②,解得a=1,b=2.(13分)
点评:本题主要考察了平面向量数量积的运算,余弦定理、两角和与差的正弦函数公式的综合应用,属于中档题.

练习册系列答案
相关题目
对于两个变量y和x进行线性相关检验,已知n是 观察值组数,r是相关系数,且已知:①n=7,r=0,9533;②n=15,r=0.301,③n=17,r=0.9991,④n=3,r=0.9950,则变量y和x具有线性相关关系的是( )
| A、①和② | B、①和③ |
| C、②和④ | D、③和④ |
已知函数f(x)=cos
cos(
+2x),则函数f(x)满足( )
| 2π |
| 3 |
| π |
| 2 |
| A、f(x)的最小正周期是2π | ||||||||||||
| B、若f(x1)=f(x2),则x1=x2 | ||||||||||||
C、f(x)的图象关于直线x=
| ||||||||||||
D、当x∈[-
|
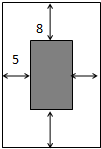 如图设计一幅矩形宣传画,要求画面(阴影部分)面积为4840cm2,画面上下边要留8cm空白,左右要留5cm空白,怎样确定画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?
如图设计一幅矩形宣传画,要求画面(阴影部分)面积为4840cm2,画面上下边要留8cm空白,左右要留5cm空白,怎样确定画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?