题目内容
9.若点(1,1)在二元一次不等式x+y+a<0所表示的平面区域内,则实数a的取值范围是a<-2.分析 根据点与二元一次不等式之间的关系,即可得到结论.
解答 解:若点(1,1)在二元一次不等式x+y+a<0所表示的平面区域内,
则点A的坐标满足不等式,
即1+1+a<0,
则a<-2,
故答案为:a<-2.
点评 本题主要考查二元一次不等式表示平面区域,利用点的坐标和二元一次不等式之间的关系是解决本题的关键.

练习册系列答案
相关题目
20.定义在(-1,1]上的函数f(x)满足f(x)+1=$\frac{1}{f(x+1)}$,当x∈[0,1]时,f(x)=x,若函数g(x)=|f(x)-$\frac{1}{2}$|-mx-m+1在(-1,1]内恰有3个零点,则实数m的取值范围是( )
| A. | ($\frac{3}{2}$,+∞) | B. | ($\frac{3}{2}$,$\frac{25}{8}$) | C. | ($\frac{3}{2}$,$\frac{25}{16}$) | D. | ($\frac{2}{3}$,$\frac{3}{4}$) |
4.若将函数y=sin(2x+φ)(0<φ<π)图象向右平移$\frac{π}{8}$个单位长度后关于y轴对称,则φ的值为( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{8}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{8}$ |
19.定义在(0,$\frac{π}{2}$),上的函数f(x),f′(x)是导函数,满足f(x)<f′(x)tanx,则下列表达式正确的是( )
| A. | $\sqrt{3}$•f($\frac{π}{4}$)>$\sqrt{2}$•f($\frac{π}{3}$) | B. | f(1)>2•f($\frac{π}{6}$)•sin1 | C. | $\sqrt{2}$•f($\frac{π}{6}$)>f($\frac{π}{4}$) | D. | $\sqrt{3}$•f($\frac{π}{6}$)>f($\frac{π}{3}$) |
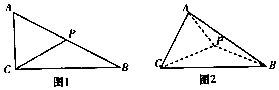 如图1,在△ABC中,AC=2,∠ACB=90°,∠ABC=30°,P是AB边的中点,现把△ACP沿CP折成如图2所示的三棱锥A-BCP,使得$AB=\sqrt{10}$.
如图1,在△ABC中,AC=2,∠ACB=90°,∠ABC=30°,P是AB边的中点,现把△ACP沿CP折成如图2所示的三棱锥A-BCP,使得$AB=\sqrt{10}$.