题目内容
某人计划间种植n棵树,已知每棵树是否成活互不影响,成活率为p(0<p<1),设ξ表示他所种植的树中成活的棵数,ξ的数学期望为Eξ,方差为Dξ.
(1)若n=1,求Dξ的最大值;
(2)已知Eξ=3,标准差σξ=
,求n,p的值并写出ξ的分布列.
(1)若n=1,求Dξ的最大值;
(2)已知Eξ=3,标准差σξ=
| ||
| 2 |
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(1)ξ表示他所种植的树中成活的棵数,当n=1,ξ的可能取值是0,1,写出ξ的分布列,根据分布列做出期望值,代入方差的公式求出方差,根据二次函数的最值求出结果.
(2)根据每棵树是否成活互不影响,成活率为p得到ξ~B(n,p),根据Eξ=np,Dξ=npq=np(1-p),求出P的值,ξ表示他所种植的树中成活的棵数,则变量的可能取值是0,1,2,3,4,根据独立重复试验概率公式写出变量的分布列.
(2)根据每棵树是否成活互不影响,成活率为p得到ξ~B(n,p),根据Eξ=np,Dξ=npq=np(1-p),求出P的值,ξ表示他所种植的树中成活的棵数,则变量的可能取值是0,1,2,3,4,根据独立重复试验概率公式写出变量的分布列.
解答:
解:(1)由题意知ξ表示他所种植的树中成活的棵数,
当n=1,ξ=0,1,于是ξ的分布列为:
∴Eξ=0×(1-p)+1×p=p.
∴Dξ=(0-p)2•(1-p)+(1-p)2•p=p-p2=-(p-
)2+
,
即当p=
时,Dξ有最大值
.
(2)每棵树是否成活互不影响,成活率为p得到ξ~B(n,p),
∴Eξ=np,Dξ=npq=np(1-p),
∴np=3,
=
,
解得p=
,n=4.
∴P(ξ=k)=
(
)k(1-
)4-k,(k=0,1,2,3,4),
∴ξ的分布列为
当n=1,ξ=0,1,于是ξ的分布列为:
| ξ | 0 | 1 |
| P | 1-p | p |
∴Dξ=(0-p)2•(1-p)+(1-p)2•p=p-p2=-(p-
| 1 |
| 2 |
| 1 |
| 4 |
即当p=
| 1 |
| 2 |
| 1 |
| 4 |
(2)每棵树是否成活互不影响,成活率为p得到ξ~B(n,p),
∴Eξ=np,Dξ=npq=np(1-p),
∴np=3,
| np(1-p) |
| ||
| 2 |
解得p=
| 3 |
| 4 |
∴P(ξ=k)=
| C | k 4 |
| 3 |
| 4 |
| 3 |
| 4 |
∴ξ的分布列为
| ξ | 0 | 1 | 2 | 3 | 4 | ||||||||||
| P |
|
|
|
|
|
点评:本题考查离散型随机变量的分布列,考查n次独立重复试验恰好发生k次的实验,考查二次函数的最值问题,考查利用概率知识解决实际问题,是一个综合题目.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
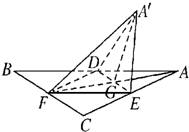 如图,等边三角形ABC的中线AF与中位线DE相交于G,已知△A′ED是△ADE绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,等边三角形ABC的中线AF与中位线DE相交于G,已知△A′ED是△ADE绕DE旋转过程中的一个图形,下列命题中,错误的是( )| A、动点A′在平面ABC上的射影在线段AF上 |
| B、恒有平面A′GF⊥平面ACDE |
| C、三棱锥′-EFD的体积有最大值 |
| D、异面直线A′E与BD不可能垂直 |
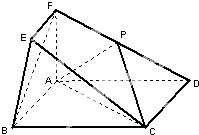 在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=1,点P在棱DF上.
在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=1,点P在棱DF上.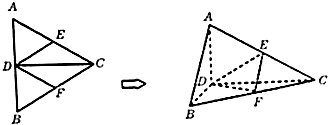
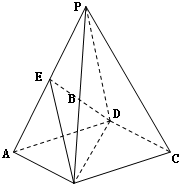 如图,在四棱柱P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥BC.求证:
如图,在四棱柱P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥BC.求证:
 如图,在⊙O的直径AB的延长线上任取一点C,过点C引直线与⊙O交于点D、E,在⊙O上再取一点F,使
如图,在⊙O的直径AB的延长线上任取一点C,过点C引直线与⊙O交于点D、E,在⊙O上再取一点F,使