题目内容
3.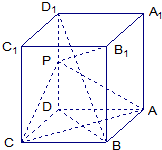 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.求:
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.求:(1)直线BD1面ABCD所成角正切值;
(2)平面PAC与面ACD所成角的正弦值.
分析 (1)由DD1⊥平面ABCD,知∠D1BD是直线BD1面ABCD所成角,由此能求出直线BD1面ABCD所成角正切值.
(2)设AC∩BD=O,连结PO,∠POD是平面PAC与面ACD所成角,由此能求出平面PAC与面ACD所成角的正弦值.
解答 解:(1)∵长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,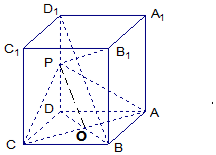
DD1⊥平面ABCD,
∴∠D1BD是直线BD1面ABCD所成角,
∴tan∠D1BD=$\frac{D{D}_{1}}{BD}$=$\frac{2}{\sqrt{{1}^{2}+{1}^{2}}}$=$\sqrt{2}$,
∴直线BD1面ABCD所成角正切值为$\sqrt{2}$.
(2)∵AB=AD=1,AA1=2,点P为DD1的中点,
∴PC=PA=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,CO=DO=$\frac{1}{2}\sqrt{{1}^{2}+{1}^{2}}$=$\frac{\sqrt{2}}{2}$,
设AC∩BD=O,连结PO,
则PO⊥AC,DO⊥AC,
∴∠POD是平面PAC与面ACD所成角,
PO=$\sqrt{P{C}^{2}-C{O}^{2}}$=$\sqrt{2-\frac{1}{2}}$=$\frac{\sqrt{6}}{2}$,
∴sin∠POD=$\frac{PD}{PO}$=$\frac{1}{\frac{\sqrt{6}}{2}}$=$\frac{\sqrt{6}}{3}$.
∴平面PAC与面ACD所成角的正弦值为$\frac{\sqrt{6}}{3}$.
点评 本题考查线面角的正切值的求法,考查面面角的正弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
16.若函数y=-ax与y=$\frac{b}{x}$在(-∞,0)上都是减函数,则y=ax2+bx在(-∞,0)上是( )
| A. | 减函数 | B. | 增函数 | C. | 先增后减 | D. | 先减后增 |
17.定义在R上的函数f(x)对任意两个不相等实数a、b,且a<b总有f(a)<f(b)成立,则必有( )
| A. | f(x)先增加后减少 | B. | f(x)先减少后增加 | C. | f(x)在R上是增函数 | D. | f(x)在R上是减函数 |
14.已知向量$\overrightarrow{a},\overrightarrow{b}$是单位向量,$\overrightarrow{a}•\overrightarrow{b}$=0,若|$\overrightarrow{c}-\overrightarrow{a}-\overrightarrow{b}$|=1,则|$\overrightarrow{c}$|的最大值为( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{2}+1$ |