题目内容
已知函数f(x)=
.
(I)求函数f(x)的单调区间;
(II)若函数f(x)在区间(t,t+
)(t>0)上不是单调函数,求实数t的取值范围;
(III)如果当x≥1时,不等式f(x)≥
恒成立,求实数a的取值范围.
| 1+lnx |
| x |
(I)求函数f(x)的单调区间;
(II)若函数f(x)在区间(t,t+
| 1 |
| 2 |
(III)如果当x≥1时,不等式f(x)≥
| a |
| x+1 |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:计算题,函数的性质及应用,导数的综合应用
分析:(I)求导f′(x)=-
,从而由导数的正负确定函数的单调区间;
(II)由f(x)的单调增区间为(0,1),单调减区间为(1,+∞)得t<1<t+
,从而解得;
(III)不等式f(x)≥
可化为a≤
,令g(x)=
,从而化恒成立为a≤gmin(x),(x≥1);从而转化为函数的最值问题.
| lnx |
| x2 |
(II)由f(x)的单调增区间为(0,1),单调减区间为(1,+∞)得t<1<t+
| 1 |
| 2 |
(III)不等式f(x)≥
| a |
| x+1 |
| (x+1)(1+lnx) |
| x |
| (x+1)(1+lnx) |
| x |
解答:
解:(I)∵f(x)=
,x>0,故f′(x)=-
,
则当x∈(0,1)时,f′(x)>0,当x∈(1,+∞)时,f′(x)<0;
故f(x)的单调增区间为(0,1),单调减区间为(1,+∞);
(II)∵f(x)的单调增区间为(0,1),单调减区间为(1,+∞);
∴t<1<t+
,
故
<t<1;
故实数t的取值范围为(
,1);
(III)不等式f(x)≥
可化为a≤
,
令g(x)=
,
则当x≥1时,不等式f(x)≥
恒成立可化为
a≤gmin(x),(x≥1);
而g′(x)=
;
令h(x)=x-lnx;则h′(x)=1-
≥0;
故h(x)在[1,+∞)上是增函数,
故h(x)≥h(1)≥1;
故g′(x)=
>0;
故g(x)=
在[1,+∞)上是增函数,
故gmin(x)=g(1)=2,
故a≤2;
故实数a的取值范围为(-∞,2].
| 1+lnx |
| x |
| lnx |
| x2 |
则当x∈(0,1)时,f′(x)>0,当x∈(1,+∞)时,f′(x)<0;
故f(x)的单调增区间为(0,1),单调减区间为(1,+∞);
(II)∵f(x)的单调增区间为(0,1),单调减区间为(1,+∞);
∴t<1<t+
| 1 |
| 2 |
故
| 1 |
| 2 |
故实数t的取值范围为(
| 1 |
| 2 |
(III)不等式f(x)≥
| a |
| x+1 |
| (x+1)(1+lnx) |
| x |
令g(x)=
| (x+1)(1+lnx) |
| x |
则当x≥1时,不等式f(x)≥
| a |
| x+1 |
a≤gmin(x),(x≥1);
而g′(x)=
| x-lnx |
| x2 |
令h(x)=x-lnx;则h′(x)=1-
| 1 |
| x |
故h(x)在[1,+∞)上是增函数,
故h(x)≥h(1)≥1;
故g′(x)=
| x-lnx |
| x2 |
故g(x)=
| (x+1)(1+lnx) |
| x |
故gmin(x)=g(1)=2,
故a≤2;
故实数a的取值范围为(-∞,2].
点评:本题了函数的综合应用及导数的综合应用,同时考查了恒成立问题,属于中档题.

练习册系列答案
相关题目
若ξ是离散型随机变量,则E(ξ-E(ξ))的值为( )
| A、E(ξ) |
| B、0 |
| C、(E(ξ))2 |
| D、2E(ξ) |
设θ为两个非零向量
,
的夹角,已知对任意实数t,|
-t
|的最小值是2,则( )
| a |
| b |
| b |
| a |
A、若θ确定,则|
| ||
B、若θ确定,则|
| ||
C、若|
| ||
D、若|
|
运行如图所示的程序框图后,输出的结果是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法不正确的是( )
| A、命题“若x>0且y>0,则x+y>0”的否命题是假命题 | ||
| B、命题“?x0∈R,x02-x0-1<0”的否定是“?x∈R,x2-x-1≥0” | ||
C、“φ=
| ||
| D、a<0时,幂函数y=xa在(0,+∞)上单调递减 |
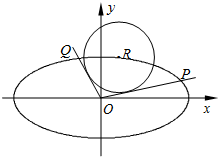 如图,在平面直角坐标系xOy中,已知椭圆C:
如图,在平面直角坐标系xOy中,已知椭圆C: