题目内容
已知△ABC的外接圆的圆心为O,满足
=m
+n
,4m+3n=2且|CB|=6,|CA|=4
,则
•
= .
| CO |
| CA |
| CB |
| 3 |
| CA |
| CB |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:在
=m
+n
两边分别乘以
,
便能够得到
,根据4m+3n=2,①+②便可得到18=(m+n)
•
③,而①×3+②×4可得,72=72(m+n)+
•
④,所以由③得,m+n=
带入④即可求出
•
.
| CO |
| CA |
| CB |
| CA |
| CB |
|
| CA |
| CB |
| CA |
| CB |
| 18 | ||||
|
| CA |
| CB |
解答:
解:如图,取AC中点D,连接OD,则OD⊥AC;
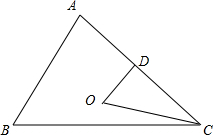
∴
•
=|
|•|
|=2
×4
=24;
同理,
•
=3×6=18;
;
∴
;
①+②得,42=12(4m+3n)+(m+n)
•
;
∴42=24+(m+n)
•
;
∴(m+n)
•
=18 ③;
①×3+②×4得,72(m+n)+
•
=72 ④;
∴③④联立可解得
•
=36.
故答案为:36.

∴
| CO |
| CA |
| CD |
| CA |
| 3 |
| 3 |
同理,
| CO |
| CB |
|
∴
|
①+②得,42=12(4m+3n)+(m+n)
| CA |
| CB |
∴42=24+(m+n)
| CA |
| CB |
∴(m+n)
| CA |
| CB |
①×3+②×4得,72(m+n)+
| CA |
| CB |
∴③④联立可解得
| CA |
| CB |
故答案为:36.
点评:考查数量积的计算公式,直角三角形中边角的关系,以及通过构造方程组求未知数
•
的方法.
| CA |
| CB |

练习册系列答案
相关题目
设θ为两个非零向量
,
的夹角,已知对任意实数t,|
-t
|的最小值是2,则( )
| a |
| b |
| b |
| a |
A、若θ确定,则|
| ||
B、若θ确定,则|
| ||
C、若|
| ||
D、若|
|
运行如图所示的程序框图后,输出的结果是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
执行如图所示的程序框图,输出的T=( )


| A、29 | B、44 | C、52 | D、62 |
下列说法不正确的是( )
| A、命题“若x>0且y>0,则x+y>0”的否命题是假命题 | ||
| B、命题“?x0∈R,x02-x0-1<0”的否定是“?x∈R,x2-x-1≥0” | ||
C、“φ=
| ||
| D、a<0时,幂函数y=xa在(0,+∞)上单调递减 |
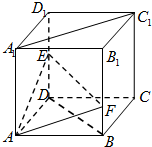 如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,
如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,