题目内容
已知数列{an}是公差大于零的等差数列,数列{bn}为等比数列,且a1=1,b1=2,b2-a2=1,a3+b3=13
(Ⅰ)求数列{an}和{bn}的通项公式
(Ⅱ)设cn=anbn+1,求数列{
}前n项和Tn.
(Ⅰ)求数列{an}和{bn}的通项公式
(Ⅱ)设cn=anbn+1,求数列{
| 1 |
| cn |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)由已知得:
,由此能求出数列{an}和{bn}的通项公式.
(Ⅱ)利用裂项求和法能求出数列{
}前n项和Tn.
|
(Ⅱ)利用裂项求和法能求出数列{
| 1 |
| cn |
解答:
(本小题满分10分)
解:(Ⅰ)设数列{an}的公差为d(d>0),数列{bn}的公比为q
由已知得:
,
解得:
,
(3分)
因为d>0,所以d=2,q=2,
∴an=1+2(n-1)=2n-1,bn=2×2n-1=2n
即an=2n-1(n∈N*),bn=2n(n∈N*).(6分)
(Ⅱ)Tn=
+
+
+…+
=
.(10分)
解:(Ⅰ)设数列{an}的公差为d(d>0),数列{bn}的公比为q
由已知得:
|
解得:
|
|
因为d>0,所以d=2,q=2,
∴an=1+2(n-1)=2n-1,bn=2×2n-1=2n
即an=2n-1(n∈N*),bn=2n(n∈N*).(6分)
(Ⅱ)Tn=
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| (2n-1)(2n+1) |
|
=
| n |
| 2n+1 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
椭圆C:
+
=1的左、右顶点分别为A1,A2,点P在C上且直线PA2的斜率的取值范围是[-3,-1],那么直线PA1斜率的取值范围是( )
| x2 |
| 4 |
| y2 |
| 3 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
tan300°+
的值是( )
| cos(-4050) |
| sin7650 |
A、1+
| ||
B、1-
| ||
C、-1-
| ||
D、-1+
|
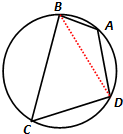 已知圆内接四边形ABCD的边AB=1,BC=3,CD=DA=2.
已知圆内接四边形ABCD的边AB=1,BC=3,CD=DA=2.