题目内容
已知集合A={-1，1，3，2m-1}，集合B={3，m2}，若B⊆A，则满足条件的实数m的集合为 ．
考点：集合的包含关系判断及应用
专题：集合
分析：根据B⊆A，B中的元素都是A中的元素，主要A中的元素不能相同．
解答：
解：因为B⊆A，
所以m2=1或m2=2m-1，
解得m=1或m=-1；m=1
当m=1时，A中有2个1，不满足集合的元素的互异性，故m≠1，
经检验知，m=-1满足题意．
故m=-1．
所以m2=1或m2=2m-1，
解得m=1或m=-1；m=1
当m=1时，A中有2个1，不满足集合的元素的互异性，故m≠1，
经检验知，m=-1满足题意．
故m=-1．
点评：本题主要考查集合间的关系，集合中元素的特点，属于基础题．
练习册系列答案
相关题目
已知m，n为不同的直线，α，β为不同的平面，则下列说法正确的是（ ）
| A、m?α，n∥m⇒n∥α |
| B、m?α，n⊥m⇒n⊥α |
| C、m?α，n?β，m∥n⇒α∥β |
| D、n?β，n⊥α⇒α⊥β |
已知条件p：x＞1或x＜-3，条件q：x＞a，且q是p的充分而不必要条件，则a的取值范围是（ ）
| A、a≥1 | B、a≤1 |
| C、a≥-3 | D、a≤-3 |
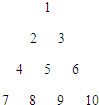把正整数按上小下大、左小右大的原则排成如图三角形数表（每行比上一行多一个数）：设ai，j（i、j∈N*）是位于这个三角形数表中从上往下数第i行、从左往右数第j个数，如a4，2=8，则a51，25为
下列说法正确的是（ ）
| A、命题“若x2=1，则x=1”的否命题是“若x2=1，则x≠1” | ||
| B、“x=-1”是“x2-x-2=0”的必要不充分条件 | ||
C、“tanx=1”是“x=
| ||
| D、命题“若x=y，则sinx=siny”的逆否命题是真命题 |