题目内容
函数f(x)的定义域为A,若x1,x2∈A,且f(x1)=f(x2)时,总有x1=x2,则称f(x)为单函数.例如:函数f(x)=2x+1(x∈R)是单函数.给出下列命题:
①函数f(x)=x2(x∈R)是单函数;
②指数函数f(x)=2x(x∈R)是单函数;
③若f(x)为单函数,x1,x2∈A且x1≠x2,则f(x1)≠f(x2);
④在定义域上具有单调性的函数一定是单函数,
其中正确命题的个数是( )
①函数f(x)=x2(x∈R)是单函数;
②指数函数f(x)=2x(x∈R)是单函数;
③若f(x)为单函数,x1,x2∈A且x1≠x2,则f(x1)≠f(x2);
④在定义域上具有单调性的函数一定是单函数,
其中正确命题的个数是( )
| A、3 | B、2 | C、1 | D、0 |
考点:命题的真假判断与应用
专题:新定义,函数的性质及应用
分析:利用单函数的定义当f(x1)=f(x2)时总有x1=x2,分别对四个命题进行判断,可以得出正确结论.
由两数的平方相等,则这两数相等或互为相反数,即可判断①;由指数函数的单调性,即可判断②;
由互为逆否命题的等价性,即可判断③;由单调性的性质,即可判断④.
由两数的平方相等,则这两数相等或互为相反数,即可判断①;由指数函数的单调性,即可判断②;
由互为逆否命题的等价性,即可判断③;由单调性的性质,即可判断④.
解答:
解:对于①,函数f(x)=x2,由f(x1)=f(x2)得x12=x22,即x1=-x2或x1=x2,所以①不是单函数,①错误;
对于②,函数f(x)=2x,由f(x1)=f(x2)即2x1=2x2,则x1=x2,所以②是单函数,②正确;
对于③,f(x)为单函数,则f(x1)=f(x2)时,有x1=x2,逆否命题是x1≠x2时,有f(x1)≠f(x2),所以③是正确的;
对于④,若函数f(x)是单调函数,则满足f(x1)=f(x2)时,有x1=x2,所以④是单函数,④正确.
故正确的是②③④.
故选A.
对于②,函数f(x)=2x,由f(x1)=f(x2)即2x1=2x2,则x1=x2,所以②是单函数,②正确;
对于③,f(x)为单函数,则f(x1)=f(x2)时,有x1=x2,逆否命题是x1≠x2时,有f(x1)≠f(x2),所以③是正确的;
对于④,若函数f(x)是单调函数,则满足f(x1)=f(x2)时,有x1=x2,所以④是单函数,④正确.
故正确的是②③④.
故选A.
点评:本题主要考查与函数有关的命题的真假判断,考查函数的性质和应用,利用单函数的定义是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
双曲线
-y2=-1的离心率为( )
| x2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知m,n为不同的直线,α,β为不同的平面,则下列说法正确的是( )
| A、m?α,n∥m⇒n∥α |
| B、m?α,n⊥m⇒n⊥α |
| C、m?α,n?β,m∥n⇒α∥β |
| D、n?β,n⊥α⇒α⊥β |
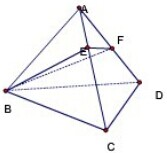 正三棱锥A-BCD底面边长为a,侧棱长为2a,E、F分别为AC,AD上的动点,求截面△BEF周长的最小值和这时E、F的位置.
正三棱锥A-BCD底面边长为a,侧棱长为2a,E、F分别为AC,AD上的动点,求截面△BEF周长的最小值和这时E、F的位置.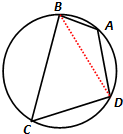 已知圆内接四边形ABCD的边AB=1,BC=3,CD=DA=2.
已知圆内接四边形ABCD的边AB=1,BC=3,CD=DA=2.