题目内容

设x＞1，求函数y=
(x-1)5
(10x-6)9
的最大值．
考点：基本不等式
专题：导数的概念及应用
分析：本题求最大值，转化为利用导数求函数的最值问题．
解答： 解：∵y=
(x-1)5
(10x-6)9
．
∴y′=-
20(x-1)4(2x-3)
(10x-6)10

令y′=0，则x=
3
2
，
当y′＞0时，即1＜x＜
3
2
，函数为增函数，
当y′＜0时，即x＞
3
2
，函数为减函数，
故x=
3
2
，函数有最大值，
ymax=
(
3
2
-1)5
(10×
3
2
-6)10
=
1
25×99
点评：本题考查了利用导数求函数的最值问题，属于中档题．
练习册系列答案
相关题目
已知-1＜a＜2，0＜b＜3，则a-b的取值范围是
 
．
设x，y满足约束条件
x+y≤1
y≤x
y≥-2
，则z=3x+y的最小值为（　　）
A、-10B、-8C、2D、7
cos（π+α）=（　　）
A、cosαB、-cosα
C、sinαD、-sinα
已知定义在区间[-1，1]上的函数f（x）=
2x+b
x2+1
为奇函数．
（1）求实数b的值．
（2）判断函数f（x）在区间（-1，1）上的单调性，并证明你的结论．
已知曲线C上任意一点P到两定点F1（-1，0）与F2（1，0）的距离之和为4．
（Ⅰ）求曲线C的方程；
（Ⅱ）设曲线C与x轴负半轴交点为A，过点M（-4，0）作斜率为k的直线l交曲线C于B、C两点（B在M、C之间），N为BC中点．
（ⅰ）证明：k•kON为定值；
（ⅱ）是否存在实数k，使得F1N⊥AC？如果存在，求直线l的方程，如果不存在，请说明理由．
已知函数f（x）=loga
mx+1
x-1
（a＞1）为奇函数
（1）求实数m的值；
（2）指出函数y=f（x）的单调区间（无需证明）；
（3）若仅有一个常数c使得对于任意的s∈[a，2014a]，都有t∈[a，a2]满足方程f(
s+1
s-1
)+f(
t+1
t-1
)=c，求实数a的值．
在（
x
2
-
1
x
）6的展开式中，求：
（1）第5项的系数；  
（2）常数项．
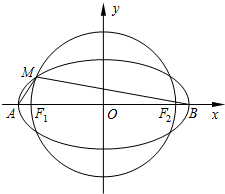如图，在平面直角坐标系xOy中，椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右顶点分别为A，B，左、右焦点分别为F1，F2，点M在椭圆上，且直线MA，MB的斜率之积为-
1
4
．
（1）求椭圆的离心率；
（2）若点M又在以线段F1F2为直径的圆上，且△MAB的面积为
2
3
3
，
求椭圆的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网