题目内容
16.已知函数f(x)=alog2x-blog3x+2,若f($\frac{1}{2015}$)=4,则f(2015)=0.分析 利用对数的运算性质,可得f($\frac{1}{2015}$)+f(2015)=4,即可求出f(2015)的值.
解答 解:由函数f(x)=alog2x-blog3x+2,
得f($\frac{1}{x}$)=-alog2x+blog3x+2
因此f(x)+f($\frac{1}{x}$)=4,
再令x=2015,得f($\frac{1}{2015}$)+f(2015)=4
所以f(2015)=4-f($\frac{1}{2015}$)=0,
故答案为:0.
点评 本题考查了对数的运算性质,和函数的简单性质,属于基础题.利用互为倒数的两个自变量的函数值之间的关系,是解决本题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
1.已知函数f(x)=2sin(ωx+$\frac{π}{6}$)(ω>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则f(x)的单调递增区间为( )
| A. | [kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$]k∈Z | B. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$]k∈Z | ||
| C. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$]k∈Z | D. | [kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$]k∈Z |
8.一个几何体的三视图如图所示,则这个几何体的体积是( )


| A. | 2 | B. | $\frac{1}{2}$ | C. | 3 | D. | $\frac{1}{3}$ |
5.已知x、y满足约束条件$\left\{\begin{array}{l}{x-y≥1}\\{2x-y+1≤0}\end{array}\right.$,且目标函数z=mx-ny(m>0,n<0)的最大值为-6,则$\frac{n}{m-1}$的取值范围是( )
| A. | [-2,0]∪[$\frac{1}{2}$,+∞) | B. | [2,+∞) | C. | (-∞,0)∪(2,+∞) | D. | (-∞,0)∪[$\frac{1}{2}$,+∞) |
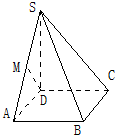 如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SD=1,SB=$\sqrt{3}$.
如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SD=1,SB=$\sqrt{3}$.