题目内容
(本小题满分12分)
设数列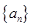 的前
的前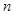 项和为
项和为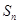 ,且方程
,且方程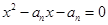 有一根为
有一根为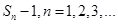
(I)求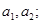 (II)求
(II)求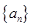 的通项公式
的通项公式
设数列
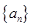 的前
的前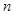 项和为
项和为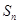 ,且方程
,且方程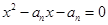 有一根为
有一根为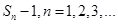
(I)求
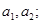 (II)求
(II)求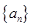 的通项公式
的通项公式(Ⅰ)当n=1时,

有一根为
 于是
于是
解得
 ……2分
……2分当n=2时,有一根为
 于是
于是
解得
 。 ……5分
。 ……5分(Ⅱ)由题设

即

当

 ①
①由(Ⅰ)知


由①可得

由此猜想
 ……8分
……8分下面用数学归纳法证明这个结论。
(i)n=1时已知结论成立。
(ii)假设n=k时结论成立,即

当n=k+1时,由①得

即
 ,
,故n=k+1时结论也成立。
综上,由(i)、(ii)可知
 对所有正整数n都成立。 ……10分
对所有正整数n都成立。 ……10分于是当

又n=1时,
 所以{
所以{ }的通项公式为
}的通项公式为 1,2,3,…。
1,2,3,…。……12分
略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 中,已知
中,已知 ,
, (
( .
. 是等差数列;
是等差数列; 及它的前
及它的前 项和
项和 .
.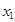 ,
,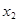 ,…,
,…,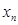 的“倒平均数”为
的“倒平均数”为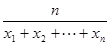 (
(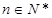 ).已知数列
).已知数列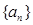 前
前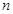 项的“倒平均数”为
项的“倒平均数”为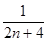 ,记
,记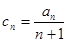 (
(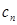 与
与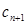 的大小;
的大小;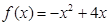 ,对(1)中的数列
,对(1)中的数列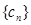 ,是否存在实数
,是否存在实数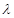 ,使得当
,使得当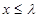 时,
时,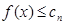 对任意
对任意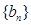 满足
满足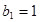 ,
,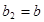 (
(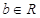 且
且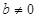 ),
),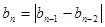 (
(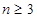 ),且
),且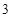 的周期数列,设
的周期数列,设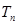 为
为 均数”,求
均数”,求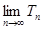 .
. 满足
满足 且
且 ,则
,则 等于 ( )
等于 ( ) 、
、
 、
、
 、
、
 、
、
 (
( )满足
)满足 ,
, ,且点
,且点 的坐标为
的坐标为 .
. 的直线
的直线 的方程;
的方程; 通项公式.
通项公式.
 成立的最大实数
成立的最大实数 的值.
的值.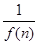 ,bn=f(
,bn=f(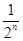 )+1.记Pn=S1S2+S2S3+…+SnSn+1,Tn=b1b2+b2b3+…+bnbn+1,试求Tn,并证明Pn<
)+1.记Pn=S1S2+S2S3+…+SnSn+1,Tn=b1b2+b2b3+…+bnbn+1,试求Tn,并证明Pn< .
. ,则S9等于( )
,则S9等于( )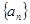 ,如果存在最小的一个常数
,如果存在最小的一个常数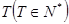 ,使得对任意的正整数恒有
,使得对任意的正整数恒有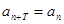 成立,则称数列
成立,则称数列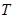 的周期数列。设
的周期数列。设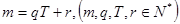 ,数列前
,数列前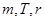 项的和分别记为
项的和分别记为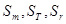 ,则
,则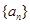 的通项公式为
的通项公式为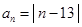 ,那么满足
,那么满足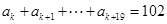 的正整数
的正整数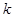 =________
=________ 的前
的前 项和为
项和为 ,
, ,且
,且 ,则
,则