题目内容
(本题满分16分)定义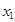 ,
,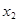 ,…,
,…,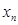 的“倒平均数”为
的“倒平均数”为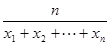 (
(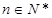 ).已知数列
).已知数列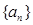 前
前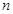 项的“倒平均数”为
项的“倒平均数”为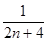 ,记
,记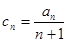 (
(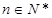 ).
).
(1)比较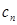 与
与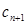 的大小;
的大小;
(2)设函数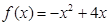 ,对(1)中的数列
,对(1)中的数列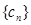 ,是否存在实数
,是否存在实数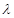 ,使得当
,使得当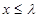 时,
时,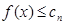 对任意
对任意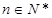 恒成立?若存在,求出最大的实数
恒成立?若存在,求出最大的实数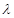 ;若不存在,说明理由.
;若不存在,说明理由.
(3)设数列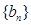 满足
满足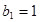 ,
,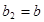 (
(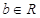 且
且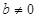 ),
),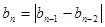 (
(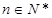 且
且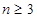 ),且
),且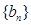 是周期为
是周期为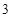 的周期数列,设
的周期数列,设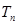 为
为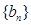 前
前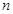 项的“倒平
项的“倒平 均数”,求
均数”,求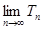 .
.
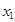 ,
,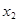 ,…,
,…,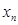 的“倒平均数”为
的“倒平均数”为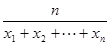 (
(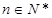 ).已知数列
).已知数列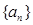 前
前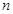 项的“倒平均数”为
项的“倒平均数”为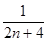 ,记
,记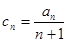 (
(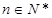 ).
).(1)比较
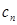 与
与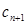 的大小;
的大小;(2)设函数
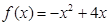 ,对(1)中的数列
,对(1)中的数列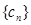 ,是否存在实数
,是否存在实数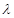 ,使得当
,使得当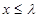 时,
时,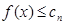 对任意
对任意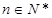 恒成立?若存在,求出最大的实数
恒成立?若存在,求出最大的实数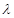 ;若不存在,说明理由.
;若不存在,说明理由.(3)设数列
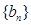 满足
满足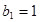 ,
,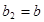 (
(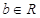 且
且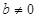 ),
),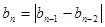 (
(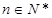 且
且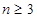 ),且
),且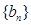 是周期为
是周期为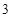 的周期数列,设
的周期数列,设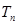 为
为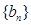 前
前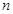 项的“倒平
项的“倒平 均数”,求
均数”,求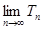 .
.(1)设数列 的前
的前 项和为
项和为 ,由题意得
,由题意得 ,
,
所以 ,……(1分)
,……(1分)
当 时,
时, ,当
,当 时,
时, ,而
,而 也满足此式.
也满足此式.
所以 (
( ).……(1分)
).……(1分)
所以 ,……(1分)
,……(1分)
 ,因此
,因此 .……(1分)
.……(1分)
(2)假设存在实数 ,使得当
,使得当 时,
时,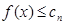 对任意
对任意 恒成立,
恒成立,
即 对任意
对任意 恒成立,……(2分)
恒成立,……(2分)
由(1)知数列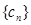 是递增数列,所以只要
是递增数列,所以只要 ,即
,即 ,(2分)
,(2分)
解得 或
或 .……(1分)
.……(1分)
所以存在最大的实数 ,使得当
,使得当 时,
时,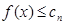 对任意
对任意 恒成立.…(1分)
恒成立.…(1分)
(3)由 ,
,
 ,得
,得 ,……(1分)
,……(1分)
① 若 ,则
,则 ,
, ,
, ,因为
,因为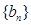 周期为
周期为 ,故
,故 ,所以
,所以 ,所以
,所以 ,
, (舍),故
(舍),故 .
.
此时,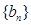 为
为 ,
, ,
, ,
, ,
, ,
, ,….符合题意.……(1分)
,….符合题意.……(1分)
② 若 ,则
,则 ,
, ,因为
,因为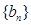 周期为
周期为 ,故
,故 ,
,
所以 ,即
,即 或
或 ,解得
,解得 或
或 ,均不合题意.…(1分)
,均不合题意.…(1分)
设数列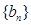 的前
的前 项和为
项和为 ,则对
,则对 ,有
,有 ……(1分)
……(1分)
即 所以
所以 因此
因此 .(2分)
.(2分)
 的前
的前 项和为
项和为 ,由题意得
,由题意得 ,
,所以
 ,……(1分)
,……(1分)当
 时,
时, ,当
,当 时,
时, ,而
,而 也满足此式.
也满足此式.所以
 (
( ).……(1分)
).……(1分)所以
 ,……(1分)
,……(1分) ,因此
,因此 .……(1分)
.……(1分)(2)假设存在实数
 ,使得当
,使得当 时,
时,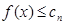 对任意
对任意 恒成立,
恒成立,即
 对任意
对任意 恒成立,……(2分)
恒成立,……(2分)由(1)知数列
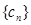 是递增数列,所以只要
是递增数列,所以只要 ,即
,即 ,(2分)
,(2分)解得
 或
或 .……(1分)
.……(1分)所以存在最大的实数
 ,使得当
,使得当 时,
时,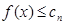 对任意
对任意 恒成立.…(1分)
恒成立.…(1分)(3)由
 ,
,
 ,得
,得 ,……(1分)
,……(1分)① 若
 ,则
,则 ,
, ,
, ,因为
,因为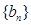 周期为
周期为 ,故
,故 ,所以
,所以 ,所以
,所以 ,
, (舍),故
(舍),故 .
.此时,
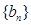 为
为 ,
, ,
, ,
, ,
, ,
, ,….符合题意.……(1分)
,….符合题意.……(1分)② 若
 ,则
,则 ,
, ,因为
,因为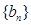 周期为
周期为 ,故
,故 ,
,所以
 ,即
,即 或
或 ,解得
,解得 或
或 ,均不合题意.…(1分)
,均不合题意.…(1分)设数列
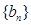 的前
的前 项和为
项和为 ,则对
,则对 ,有
,有 ……(1分)
……(1分)即
 所以
所以 因此
因此 .(2分)
.(2分)略

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
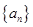 满足
满足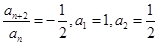 ,则
,则 。
。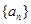 的公差
的公差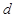 大于0,且
大于0,且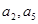 是方程
是方程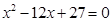 的两根,数列
的两根,数列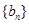 的前
的前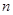 项和为
项和为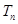 ,且
,且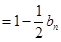
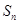 ,试比较
,试比较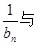
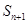 的大小,并说明理由.
的大小,并说明理由. 满足
满足
 ,若
,若 ,则
,则 的值为
的值为



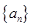 的前
的前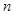 项和为
项和为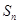 ,且方程
,且方程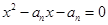 有一根为
有一根为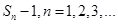
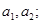 (II)求
(II)求 满足
满足 ,若
,若 ,则
,则




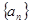 的前
的前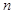 项和为
项和为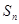 ,点
,点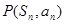 在直线
在直线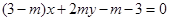 上,(
上,(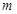 为常数,
为常数,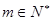 ,
,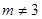 ).
).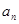 ;
;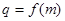 ,数列
,数列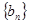 满足
满足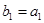 ,
,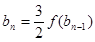 ,
,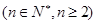 ,求证:
,求证: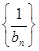 为等差
为等差 数列,并求
数列,并求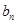 ;
;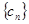 满足
满足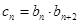 ,
,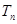 为数列
为数列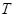 满足
满足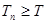
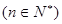 ,求
,求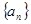 中,
中,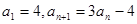 ,则数列
,则数列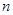 项和
项和 = .
= . 则
则 ▲
▲