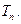题目内容
(本小题满分14分)
设数列{an}的前n项和为Sn,已知a1=1,且an+2SnSn-1=0(n≥2),
(1)求数列{Sn}的通项公式;
(2)设Sn=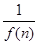 ,bn=f(
,bn=f(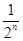 )+1.记Pn=S1S2+S2S3+…+SnSn+1,Tn=b1b2+b2b3+…+bnbn+1,试求Tn,并证明Pn<
)+1.记Pn=S1S2+S2S3+…+SnSn+1,Tn=b1b2+b2b3+…+bnbn+1,试求Tn,并证明Pn< .
.
设数列{an}的前n项和为Sn,已知a1=1,且an+2SnSn-1=0(n≥2),
(1)求数列{Sn}的通项公式;
(2)设Sn=
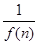 ,bn=f(
,bn=f(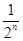 )+1.记Pn=S1S2+S2S3+…+SnSn+1,Tn=b1b2+b2b3+…+bnbn+1,试求Tn,并证明Pn<
)+1.记Pn=S1S2+S2S3+…+SnSn+1,Tn=b1b2+b2b3+…+bnbn+1,试求Tn,并证明Pn< .
.(1)解:∵an+2SnSn-1=0(n≥2),
∴Sn-Sn-1+2SnSn-1=0. ---------3分
∴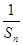 -
- =2.又∵a1=1 , ---------------5分
=2.又∵a1=1 , ---------------5分
∴Sn=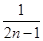 (n∈N+). ---------------7分
(n∈N+). ---------------7分
(2)证明:∵Sn=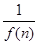 ,∴f(n)=2n-1.--------------------------8分
,∴f(n)=2n-1.--------------------------8分
∴bn=2(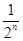 )-1+1=(
)-1+1=( )n-1.---------------------------------------9分
)n-1.---------------------------------------9分
Tn=( )0·(
)0·( )1+(
)1+( )1·(
)1·( )2+…+(
)2+…+( )n-1·(
)n-1·( )n
)n
=( )1+(
)1+( )3+(
)3+( )5+…+(
)5+…+( )2n-1
)2n-1
= [1-(
[1-( )n].-------------------------------------------------------11分
)n].-------------------------------------------------------11分

∴Sn-Sn-1+2SnSn-1=0. ---------3分
∴
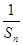 -
- =2.又∵a1=1 , ---------------5分
=2.又∵a1=1 , ---------------5分∴Sn=
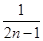 (n∈N+). ---------------7分
(n∈N+). ---------------7分(2)证明:∵Sn=
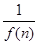 ,∴f(n)=2n-1.--------------------------8分
,∴f(n)=2n-1.--------------------------8分∴bn=2(
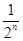 )-1+1=(
)-1+1=( )n-1.---------------------------------------9分
)n-1.---------------------------------------9分Tn=(
 )0·(
)0·( )1+(
)1+( )1·(
)1·( )2+…+(
)2+…+( )n-1·(
)n-1·( )n
)n=(
 )1+(
)1+( )3+(
)3+( )5+…+(
)5+…+( )2n-1
)2n-1=
 [1-(
[1-( )n].-------------------------------------------------------11分
)n].-------------------------------------------------------11分
略

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 1=1,an+1=2an+1(n∈N*)
1=1,an+1=2an+1(n∈N*) {an+1}是等比数列;
{an+1}是等比数列;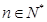 时,
时,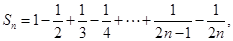
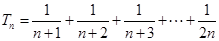 .
.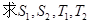 ;(II)
;(II) .
. 的前
的前 项和为
项和为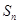 ,且方程
,且方程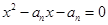 有一根为
有一根为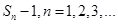
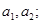 (II)求
(II)求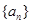 中,
中,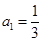 ,前
,前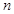 项和
项和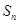 满足
满足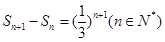 。
。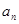 ,以及前
,以及前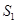 ,
,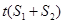 ,
,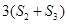 成等差数列,求实数
成等差数列,求实数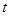 的值。
的值。 所表示的平面区域为
所表示的平面区域为 ,记
,记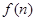 (
(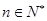 ).
).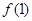 、
、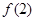 的值及
的值及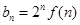 ,
,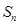 为
为 的前
的前 项和,求
项和,求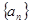 的前
的前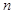 项和为
项和为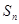 ,点
,点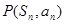 在直线
在直线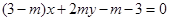 上,(
上,(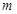 为常数,
为常数,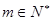 ,
,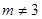 ).
).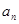 ;
;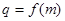 ,数列
,数列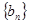 满足
满足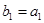 ,
,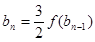 ,
,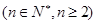 ,求证:
,求证: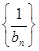 为等差
为等差 数列,并求
数列,并求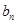 ;
;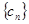 满足
满足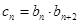 ,
,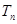 为数列
为数列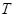 满足
满足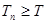
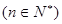 ,求
,求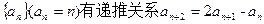 ;
;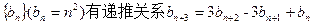 ;
;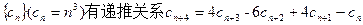 ;
;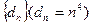 的类似的递推关系
的类似的递推关系 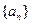 的前
的前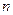 项和为
项和为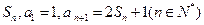 ,等差数列
,等差数列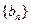 中,
中,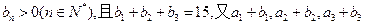 成等比数列。
成等比数列。 (2)求数列
(2)求数列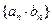 的前
的前