题目内容
12.已知直线ax+y-1=0与圆C:(x-1)2+(y+a)2=1相交于A,B两点,且△ABC为等腰直角三角形,则实数a的值为-1或1.分析 由三角形ABC为等腰直角三角形,得到圆心C到直线的距离d=rsin45°,利用点到直线的距离公式列出方程,求出方程的解即可得到a的值.
解答 解:∵由题意得到△ABC为等腰直角三角形,
∴圆心C(1,-a)到直线ax+y-1=0的距离d=rsin45°,即$\frac{|a-a-1|}{\sqrt{1+{a}^{2}}}$=$\frac{\sqrt{2}}{2}$,
整理得:1+a2=2,即a2=1,
解得:a=-1或1,
故答案为:-1或1
点评 此题考查了直角与圆的位置关系,涉及的知识有:点到直线的距离公式,圆的标准方程,等腰直角三角形的性质,以及锐角三角函数定义,熟练掌握公式及性质是解本题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
3.下列说法正确的是( )
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | 命题“?x≥0,x2+x-1<0”的否定是“?x<0,x2+x-1<0” | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 | |
| D. | 若命题p为真命题,则命题¬p也可能为真命题 |
20.若某几何体的三视图如图所示,则此几何体的表面积为( )
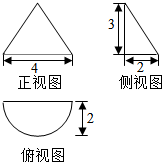

| A. | $(4+2\sqrt{13})π$ | B. | $6+(2+\sqrt{13})π$ | C. | $(\sqrt{13}+2)π$ | D. | $8+2\sqrt{13}π$ |
7.函数y=3cos2x-4cosx+1,x∈[0,$\frac{π}{2}$]的最小值为( )
| A. | $-\frac{1}{3}$ | B. | 0 | C. | $\frac{1}{3}$ | D. | 1 |
17.某三棱锥的三视图如图所示,则该三棱锥四个面中,为直角三角形的个数为( )
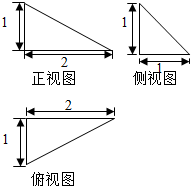

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |