题目内容
已知函数f(x)=x|x-a|+x在R上为单调函数,则a的取值范围是 .
考点:函数单调性的性质
专题:计算题,函数的性质及应用
分析:先把f(x)化为分段函数,由抛物线图象开口方向可知f(x)在R上递增,借助对称轴及x的范围可得不等式组,解出可得答案.
解答:
解:f(x)=x|x-a|+x=
,
可知f(x)在R上为单调增函数,
则由题意可得,
,解得-1≤a≤1,
故答案为:-1≤a≤1.
|
可知f(x)在R上为单调增函数,
则由题意可得,
|
故答案为:-1≤a≤1.
点评:该题考查绝对值函数的单调性及二次函数的单调性问题,考查数形结合思想,考查学生分析解决问题的能力.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
一辆中型客车的营运总利润y(单位:万元)与营运年数x(x∈N)的变化关系如下表所示,要使总利润达到最大值,则该客车的营运年数是( )
| x(年) | 4 | 6 | 8 | … |
| y=ax2+bx+c | 7 | 11 | 7 | … |
| A、15 | B、10 | C、9 | D、6 |
若函数f(x)=x2+mx+1有两个不同的零点,则实数m的取值范围是( )
| A、(-1,1) |
| B、(-2,2) |
| C、(-∞,-2)∪(2,+∞) |
| D、(-∞,-2)∪(1,+∞) |
已知x+y=6,则z=x+y+xy最大值是( )
| A、13 | B、14 | C、15 | D、16 |
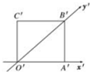 如图,正方形O′A′B′C′的边长为acm(a>0),它是一个水平放置的平面图形的直观图,则它的原图形OABC的周长是
如图,正方形O′A′B′C′的边长为acm(a>0),它是一个水平放置的平面图形的直观图,则它的原图形OABC的周长是 如图,已知边长为1的正方形ABCD位于第一象限,且顶点A、D分别在x,y的正半轴上(含原点)滑动,则
如图,已知边长为1的正方形ABCD位于第一象限,且顶点A、D分别在x,y的正半轴上(含原点)滑动,则