题目内容
已知命题p:“复数z=(λ2-1)+(λ2-2λ-3)i,(λ∈R)是实数”,命题q:“在复平面C内,复数z=λ+(λ2+λ-6)i,(λ∈R)所对应的点在第三象限”.
(1)若命题p是真命题,求λ的值;
(2)若“¬p∧q”是真命题,求λ的取值范围.
(1)若命题p是真命题,求λ的值;
(2)若“¬p∧q”是真命题,求λ的取值范围.
考点:复合命题的真假,复数的代数表示法及其几何意义
专题:简易逻辑
分析:(1)根据复数的概念,即可求λ的值;
(2)根据¬p∧q是真命题,得到命题p,q的真假,即可求λ的取值范围.
(2)根据¬p∧q是真命题,得到命题p,q的真假,即可求λ的取值范围.
解答:
解:(1)若命题p是真命题,即复数z=(λ2-1)+(λ2-2λ-3)i,(λ∈R)是实数.
则λ2-2λ-3=0,解得λ=3或λ=-1.
(2)若复数z=λ+(λ2+λ-6)i,(λ∈R)所对应的点在第三象限,
则
,即
,解得-3<λ<0,
若¬p∧q为真命题,
则¬p,q都为真命题,
即p是假命题,q是真命题.
即¬p:λ≠3且λ≠-1,
则
,
解得-3<λ<-1或-1<λ<0.
则λ2-2λ-3=0,解得λ=3或λ=-1.
(2)若复数z=λ+(λ2+λ-6)i,(λ∈R)所对应的点在第三象限,
则
|
|
若¬p∧q为真命题,
则¬p,q都为真命题,
即p是假命题,q是真命题.
即¬p:λ≠3且λ≠-1,
则
|
解得-3<λ<-1或-1<λ<0.
点评:本题主要考查复合命题的真假判断,根据条件判断p,q的真假是解决本题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
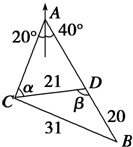 C位于A城的南偏西20°的位置,B位于A城的南偏东40°的位置,有一人距C为31千米的B处正沿公路向A城走去,走了20千米后到达D处,此时CD间的距离为21千米,问这人还要走多少千米才能到达A城?
C位于A城的南偏西20°的位置,B位于A城的南偏东40°的位置,有一人距C为31千米的B处正沿公路向A城走去,走了20千米后到达D处,此时CD间的距离为21千米,问这人还要走多少千米才能到达A城?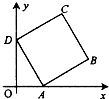 如图,边长为2的正方形ABCD的顶点A,D,分别在x轴,y轴正半轴上移动,则
如图,边长为2的正方形ABCD的顶点A,D,分别在x轴,y轴正半轴上移动,则