题目内容
18.已知边长为a的菱形ABCD中,∠ABC=60°,将该菱形沿对角线AC折起,使BD=a,则三棱锥D-ABC的体积为( )| A. | $\frac{a^3}{6}$ | B. | $\frac{a^3}{12}$ | C. | $\frac{{\sqrt{3}}}{12}{a^3}$ | D. | $\frac{\sqrt{2}}{12}{a}^{3}$ |
分析 由题意可得:三棱锥B-ACD是一个正四面体.如图所示,进而算出高BO,即可计算出体积.
解答 解:由题意可得:三棱锥B-ACD是一个棱长为a的正四面体.如图所示: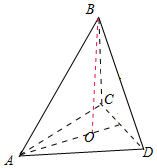
过B点作BO⊥底面ACD,则点O是底面的中心,可知AO=$\frac{2}{3}×\frac{\sqrt{3}}{2}a=\frac{\sqrt{3}}{3}a$.
在Rt△ABO中,由勾股定理得BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=$\sqrt{{a}^{2}-(\frac{\sqrt{3}}{3}a)^{2}}$=$\frac{\sqrt{6}}{3}a$.
∴V=$\frac{1}{3}×\frac{1}{2}×a×a×sin60°×\frac{\sqrt{6}}{3}a$=$\frac{\sqrt{2}}{12}{a}^{3}$.
故选:D.
点评 本题考查三棱锥的体积的求法,考查三棱锥、折叠等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、函数与方程思想、数形结合思想,是中档题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
13.设f(x)=(ax+b)sinx+(cx+d)cosx,若f'(x)=xcosx,则a,b,c,d的值分别为( )
| A. | 1,1,0,0 | B. | 1,0,1,0 | C. | 0,1,0,1 | D. | 1,0,0,1 |
10.设x>0,则$y=x+\frac{4}{x^2}$的最小值为( )
| A. | 2 | B. | $2\sqrt{2}$ | C. | 3 | D. | $3\sqrt{2}$ |
8.若$\overrightarrow{OA}$=$\overrightarrow a$,$\overrightarrow{OB}$=$\overrightarrow b$,$\overrightarrow a$与$\overrightarrow b$不共线,则∠AOB平分线上的向量$\overrightarrow{OM}$为( )
| A. | $\frac{\overrightarrow a}{{|{\overrightarrow a}|}}+\frac{\overrightarrow b}{{|{\overrightarrow b}|}}$ | B. | $\frac{\overrightarrow a+\overrightarrow b}{{|{\overrightarrow a+\overrightarrow b}|}}$ | ||
| C. | $\frac{{|{\overrightarrow b}|\overrightarrow a-|{\overrightarrow a}|\overrightarrow b}}{{|{\overrightarrow a}|+|{\overrightarrow b}|}}$ | D. | $λ(\frac{\overrightarrow a}{{|{\overrightarrow a}|}}+\frac{\overrightarrow b}{{|{\overrightarrow b}|}})$,λ由$\overrightarrow{OM}$确定 |