题目内容
1．已知函数f（x）=$\left\{\begin{array}{l}{2-x，x＞a}\\{{x}^{2}+3x+2，x≤a}\end{array}\right.$恰有三个不同的零点，则实数a的取值范围是（ ）| A． | [-2，2） | B． | [-1，2） | C． | （-2，-1] | D． | （-1，2] |
分析 由题意可得需使指数函数部分与x轴有一个交点，抛物线部分与x轴有两个交点，由函数图象的平移和二次函数的顶点可得关于a的不等式，解之可得答案．
解答 解：由题意可知：函数图象的右半部分为单调递减一次函数的部分，最多一个零点，
函数图象的左半部分为开口向上的抛物线，对称轴为x=-$\frac{3}{2}$，最多两个零点，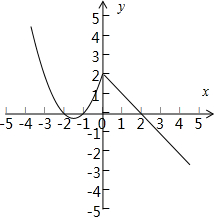
如上图，要满足题意，必须指数函数的部分向下平移到与x轴相交，
由一次函数过点（2，0），二次函数的零点为：-2．-1，
函数f（x）=$\left\{\begin{array}{l}{2-x，x＞a}\\{{x}^{2}+3x+2，x≤a}\end{array}\right.$恰有三个不同的零点，-1≤a＜2，
故选：B．
点评 本题考查根的存在性及根的个数的判断，数形结合是解决问题的关键，属中档题．
练习册系列答案
相关题目
11．抛物线y2=2px的准线经过点（-2，0），则该抛物线的焦点坐标为（ ）
| A． | （-2，0） | B． | （2，0） | C． | （0，-1） | D． | （0，1） |
如图，在四棱锥P-ABCD中，PA=PB，PA⊥PB，AB⊥BC，且平面PAB⊥平面ABCD，若AB=2，BC=1，$AD=BD=\sqrt{5}$．
16．
如图所示是求等比数列前n项和的流程图，则空白处应填（ ）
如图所示是求等比数列前n项和的流程图，则空白处应填（ ）| A． | q=1 | B． | q≠1 | C． | q＞1 | D． | q＜1 |
12．若关于x的不等式2x3+3x2-12x+4≤$\frac{4m{e}^{x}+2x}{{e}^{x}}$在[-2，+∞）上有解，则实数m 的最小值为（ ）
| A． | -$\frac{3}{4}$-$\frac{1}{e}$ | B． | -$\frac{3}{4}$-$\frac{1}{2e}$ | C． | -$\frac{4}{3}$-$\frac{1}{e}$ | D． | -$\frac{4}{3}$-$\frac{1}{2e}$ |