题目内容
2.已知函数y=Acos(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<$\frac{π}{2}$,则( )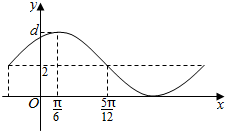
| A. | A=4 | B. | ω=1 | C. | B=4 | D. | φ=-$\frac{π}{3}$ |
分析 由函数的图象的顶点坐标求出A和B,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
解答 解:根据函数y=Acos(ωx+φ)+B的一部分图象,可得B=2,A=4-2=2,
$\frac{1}{4}$•$\frac{2π}{ω}$=$\frac{5π}{12}$-$\frac{π}{6}$,求得ω=2.
再根据五点法作图可得2•$\frac{π}{6}$+φ=0,求得φ=-$\frac{π}{3}$,∴y=2cos(2x-$\frac{π}{3}$)+2,
故选:D.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,属于基础题.

练习册系列答案
相关题目
17.方程x2+y2+2ax-4y+(a2+a)=0表示一个圆,则a的取值范围是( )
| A. | [4,+∞) | B. | (4,+∞) | C. | (-∞,4] | D. | (-∞,4) |
14.把函数y=sin3x的图象向右平移$\frac{π}{4}$个长度单位,所得曲线的对应函数式( )
| A. | y=sin(3x-$\frac{3π}{4}$) | B. | y=sin(3x+$\frac{π}{4}$) | C. | y=sin(3x-$\frac{π}{4}$) | D. | y=sin(3x+$\frac{3π}{4}$) |