题目内容
7.sin43°cos2°+cos43°sin2°的值为$\frac{\sqrt{2}}{2}$.分析 由条件利用两角和的正弦公式,求得sin43°cos2°+cos43°sin2°的值.
解答 解:sin43°cos2°+cos43°sin2°=sin(43°+2°)=sin45°=$\frac{\sqrt{2}}{2}$,
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题主要考查两角和的正弦公式的应用,属于基础题.

练习册系列答案
相关题目
17.如果直线3ax-by+15=0(a>0,b>0)和函数f(x)=mx+1+2(m>0,m≠1)的图象恒过同一个定点,且该定点始终落在圆(x-a+1)2+(y+b-3)2=16的内部或圆上,那么,$\frac{a}{b}$的取值范围是( )
| A. | [$\frac{16-5\sqrt{7}}{9}$,$\frac{16+5\sqrt{7}}{9}$) | B. | ($\frac{16-5\sqrt{7}}{9}$,$\frac{16+5\sqrt{7}}{9}$) | C. | [$\frac{16-5\sqrt{7}}{9}$,$\frac{16+5\sqrt{7}}{9}$] | D. | ($\frac{16-5\sqrt{7}}{9}$,$\frac{16+5\sqrt{7}}{9}$] |
15.设函数$f(x)={({\frac{1}{3}})^x}$与g(x)=3-x的图象的交点为( x0,y0 ),则x0所在的区间为( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
2.已知函数y=Acos(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<$\frac{π}{2}$,则( )
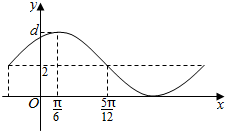

| A. | A=4 | B. | ω=1 | C. | B=4 | D. | φ=-$\frac{π}{3}$ |