题目内容

11．设复数z=x+yi（x，y∈R且y≠0），设μ=x+yi+$\frac{x-yi}{{x}^{2}+{y}^{2}}$，且-1＜μ＜2，求|z|的值及Rez的取值范围．

分析 由题意可得y-$\frac{y}{{x}^{2}+{y}^{2}}$=0且-1＜x+$\frac{x}{{x}^{2}+{y}^{2}}$＜2，结合复数的基本概念可得．

解答 解：∵复数z=x+yi（x，y∈R且y≠0），
∴μ=x+yi+$\frac{x-yi}{{x}^{2}+{y}^{2}}$=（x+$\frac{x}{{x}^{2}+{y}^{2}}$）+（y-$\frac{y}{{x}^{2}+{y}^{2}}$）i，
∵-1＜μ＜2，∴y-$\frac{y}{{x}^{2}+{y}^{2}}$=0且-1＜x+$\frac{x}{{x}^{2}+{y}^{2}}$＜2，
∴x2+y2=1，-1＜2x＜2，解得-$\frac{1}{2}$＜x＜1，
∴|z|=$\sqrt{{x}^{2}+{y}^{2}}$=1，Rez=x∈（-$\frac{1}{2}$，1）

点评 本题考查复数的模和基本概念，属基础题．

练习册系列答案
相关题目
1．已知数列{an}满足an•an-2=an-1（n＞2，n∈N），且a1=2，a2=3，则a2012=（　　）
A．$\frac{1}{3}$B．$\frac{2}{3}$C．2D．3
2．已知函数y=Acos（ωx+φ）+B的一部分图象如图所示，如果A＞0，ω＞0，|φ|＜$\frac{π}{2}$，则（　　）
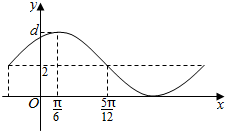
A．A=4B．ω=1C．B=4D．φ=-$\frac{π}{3}$
19．已知f（x）为偶函数，当x≥0时，f（x）=-（x-1）2+1，则满足f[f（a）+$\frac{1}{2}$]=$\frac{1}{2}$的实数a的个数为（　　）
A．2B．4C．6D．8
6．命题“?x∈R，x2-2x+1＜0”的否定形式为?x0∈R，x${\;}_{0}^{2}$-2x0+1≥0．
16．已知sinx+siny=$\frac{2}{3}$，则$\frac{1}{6}$+siny-$\frac{1}{2}$cos2x的取值范围是[$\frac{1}{12}$，$\frac{7}{9}$]．
3．设f（x）=log${\;}_{\frac{1}{2}}$（2sin$\frac{x}{2}$）．
（1）求这个函数的单调递减区间；
（2）求使f（x）＜0的x的取值范围．
20．已知向量|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=4，|$\overrightarrow{c}$|=1，（$\overrightarrow{a}-\overrightarrow{c}$）•（$\overrightarrow{b}-\overrightarrow{c}$）=$\overrightarrow{0}$，则|$\overrightarrow{a}-\overrightarrow{b}$|的最大值为$\sqrt{34}$．
1．已知sinα=-$\frac{3}{5}$，α是第四象限角，求sin（$\frac{π}{4}$-α），cos（$\frac{π}{4}$+α），tan（$α-\frac{π}{4}$）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网