题目内容
12.(Ⅰ)求右焦点坐标是(2,0),且经过点$(-2,-\sqrt{2})$的椭圆的标准方程(Ⅱ)求与椭圆$\frac{x^2}{25}+\frac{y^2}{5}=1$共焦点且过点$(3\sqrt{2},2\sqrt{2})$的双曲线的标准方程.
分析 (Ⅰ)设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,根据椭圆的简单性质,及已知点坐标列出方程组,求出a2与b2的值,即可确定出椭圆的标准方程;
(Ⅱ)由已知椭圆方程找出a与b的值,进而求出c的值,即为双曲线方程c的值,设双曲线解析式为$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{{n}^{2}}$=1,利用双曲线的简单性质及已知点坐标,求出m2与n2的值,即可确定出双曲线解析式.
解答 解:(Ⅰ)设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,
根据题意得:$\left\{\begin{array}{l}{{a}^{2}-{b}^{2}=4}\\{\frac{4}{{a}^{2}}+\frac{2}{{b}^{2}}=1}\end{array}\right.$,
解得:a2=8,b2=4,
则所求椭圆方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1;
(Ⅱ)由椭圆方程得:a=5,b=$\sqrt{5}$,
∴c=$\sqrt{{a}^{2}-{b}^{2}}$=2$\sqrt{5}$,
设双曲线解析式为$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{{n}^{2}}$=1,
可得$\left\{\begin{array}{l}{{m}^{2}+{n}^{2}=20}\\{\frac{18}{{m}^{2}}-\frac{8}{{n}^{2}}=1}\end{array}\right.$,
解得:m2=n2=10,
则双曲线解析式为$\frac{{x}^{2}}{10}$-$\frac{{y}^{2}}{10}$=1.
点评 此题考查了椭圆的标准方程,以及双曲线的标准方程,熟练掌握各自的简单性质是解本题的关键.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案| A. | [$\frac{16-5\sqrt{7}}{9}$,$\frac{16+5\sqrt{7}}{9}$) | B. | ($\frac{16-5\sqrt{7}}{9}$,$\frac{16+5\sqrt{7}}{9}$) | C. | [$\frac{16-5\sqrt{7}}{9}$,$\frac{16+5\sqrt{7}}{9}$] | D. | ($\frac{16-5\sqrt{7}}{9}$,$\frac{16+5\sqrt{7}}{9}$] |
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | 3 |
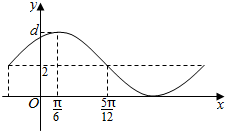
| A. | A=4 | B. | ω=1 | C. | B=4 | D. | φ=-$\frac{π}{3}$ |