题目内容
14.Sn为等比数列{an}的前n项和,且S3=2,S6=6,则a4+a5+…+a12=28.分析 由等比数列的性质可得:S3,S6-S3,S9-S6,S12-S9,仍然为等比数列.解出即可得出.
解答 解:由等比数列的性质可得:S3,S6-S3,S9-S6,S12-S9,仍然为等比数列.
∴$({S}_{6}-{S}_{3})^{2}$=S3•(S9-S6),(S6-S3)(S12-S9)=$({S}_{9}-{S}_{6})^{2}$,
又S3=2,S6=6,
解得S9=14,S12=30.
则a4+a5+…+a12=S12-S3=28.
故答案为:28.
点评 本题考查了等比数列的通项公式与求和公式及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
9.对任意实数a,b,c,d,定义符号$(\begin{array}{l}{a}&{b}\\{c}&{d}\end{array})$=$\left\{\begin{array}{l}{\sqrt{ad-bc}(ad≥bc)}\\{\frac{1}{2}\sqrt{bc-ad}(ad<bc)}\end{array}\right.$,已知函数f(x)=$(\begin{array}{l}{x}&{4}\\{1}&{x}\end{array})$,直线l:kx-y+3-2k=0,若直线l与函数f(x)的图象有两个公共点,则实数k的取值范围是( )
| A. | (-1,$\frac{2}{3}$)∪($\frac{3}{4}$,1) | B. | (-1,$\frac{17}{24}$) | C. | (-1,$\frac{17}{24}$)∪($\frac{3}{4}$,1) | D. | (-1,1) |
6.已知关于x的方程${({\frac{1}{2}})^x}-{x^{\frac{1}{3}}}=0$,那么在下列区间中含有方程的根的是( )
| A. | $(0,\frac{1}{3})$ | B. | $(\frac{1}{3},\frac{1}{2})$ | C. | $(\frac{1}{2},\frac{2}{3})$ | D. | $(\frac{2}{3},1)$ |
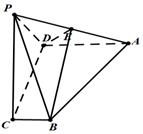 如图所示,四棱锥P-ABCD的底面为一直角梯形,BC⊥CD,CD⊥AD,AD=2BC,PC⊥底面ABCD,E为PA的中点.
如图所示,四棱锥P-ABCD的底面为一直角梯形,BC⊥CD,CD⊥AD,AD=2BC,PC⊥底面ABCD,E为PA的中点.