题目内容
5.已知f(x)=$\frac{{-{2^x}+n}}{{{2^{x+1}}+m}}$是定义在R上的奇函数.(1)求n,m的值;
(2)若对任意的c∈(-1,1),不等式f(4c-2c+1)+f(2•4c-k)<0恒成立,求实数k的取值范围.
分析 (1)根据函数的奇偶性得到f(0)=0,求出n的值,由f(1)+f(-1)=0,求出m的值,再检验即可;
(2)问题等价于f(t2-2t)<f(2t2-k)=f(k-2t2),得到k<3t2-2t,$t∈(\frac{1}{2},2)$,根据二次函数的性质求出k的范围即可.
解答 解:(1)∵f(x)是R上的奇函数,
∴f(0)=0,即$\frac{n-1}{2+m}=0$,∴n=1,
∴$f(x)=\frac{{1-{2^x}}}{{{2^{x+1}}+m}}$,又f(1)+f(-1)=0,
∴$\frac{1-2}{4+m}+\frac{{1-\frac{1}{2}}}{1+m}=0$,∴m=2.
检验:当m=2,n=1时,满足f(-x)=-f(x),
即f(x)是R上的奇函数.
(2)由(1)知$f(x)=\frac{{1-{2^x}}}{{2+{2^{x+1}}}}=-\frac{1}{2}+\frac{1}{{{2^x}+1}}$,
易知f(x)在R上为减函数,
令2c=t,因为c∈(-1,1),故$t∈(\frac{1}{2},2)$,
又f(x)是奇函数,∴f(t2-2t)+f(2t2-k)<0,
等价于f(t2-2t)<f(2t2-k)=f(k-2t2)
又因f(x)为减函数,由上式推得t2-2t>k-2t2,
即对一切$t∈(\frac{1}{2},2)$,有3t2-2t-k>0恒成立,
∴k<3t2-2t,$t∈(\frac{1}{2},2)$,
令y=3t2-2t,$t∈(\frac{1}{2},2)$,
计算得$y∈(-\frac{1}{4},8)$,
即$k≤-\frac{1}{4}$.
点评 本题考查了函数的奇偶性问题,考查函数的单调性以及转化思想,考查二次函数的性质,是一道中档题.

 53随堂测系列答案
53随堂测系列答案| A. | 若m∥α,α∥β则m∥β | B. | m∥α,m∥n则n∥α | C. | 若m∥α,n⊥α则m⊥n | D. | 若m∥α,n?α则m∥n |
| A. | $\frac{π}{15}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{16}$ | D. | $\frac{π}{18}$ |
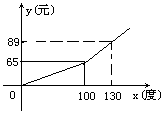 西部大部分地区的电力紧缺,电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
西部大部分地区的电力紧缺,电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题: