题目内容
19．设A={（x，y）|0＜x＜e，0＜y＜1}（e为自然对数的底数），任取（a，b）∈A，则满足ab＞1的概率是$\frac{1}{e}$（结果用e表示）．分析 根据题意，画出A表示的平面区域和满足ab＞1表示的平面区域，求出对应的面积比即可．
解答 解：画出A={（x，y）|0＜x＜e，0＜y＜1}表示的平面区域，
任取（a，b）∈A，则满足ab＞1的平面区域为图中阴影部分，
如图所示；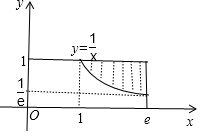
计算阴影部分的面积为
S阴影=${∫}_{1}^{e}$$\frac{1}{x}$dx=lnx${|}_{1}^{e}$=1-0=1；
所求的概率为P=$\frac{{S}_{阴影}}{{S}_{矩形}}$=$\frac{1}{1×e}$=$\frac{1}{e}$．
故答案为：$\frac{1}{e}$．
点评 本题考查了几何概型的计算问题，解题的关键是利用定积分求出阴影部分的面积．
练习册系列答案
相关题目
10．角12°化为弧度是（ ）
| A． | $\frac{π}{15}$ | B． | $\frac{π}{12}$ | C． | $\frac{π}{16}$ | D． | $\frac{π}{18}$ |