题目内容
已知点P（x，y）是直线kx+y+4=0上一动点，PA，PB是圆C：x2+y2-2y=0的两条切线，A，B为切点，若四边形PACB的最小面积是2，则k的值为 ．
考点：圆的切线方程
专题：计算题,直线与圆
分析：由圆的方程为求得圆心C，半径r，由“若四边形面积最小，则圆心与点P的距离最小时，即距离为圆心到直线的距离时，切线长PA，PB最小”，最后利用点到直线的距离求出直线的斜率即可．．
解答：
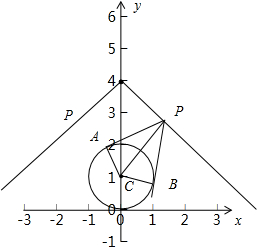解：∵圆的方程为：x2+（y-1）2=1，
∴圆心C（0，1），半径r=1．
根据题意，若四边形面积最小，当圆心与点P的距离最小时，即距离为圆心到直线l的距离最小时，切线长PA，PB最小．切线长为2，
∴PA=PB═2，
∴圆心到直线l的距离为d=
．
∵直线kx+y+4=0，
∴
=
，解得k=±2，
所求直线的斜率为：±2．
故答案为：±2
解：∵圆的方程为：x2+（y-1）2=1，∴圆心C（0，1），半径r=1．
根据题意，若四边形面积最小，当圆心与点P的距离最小时，即距离为圆心到直线l的距离最小时，切线长PA，PB最小．切线长为2，
∴PA=PB═2，
∴圆心到直线l的距离为d=
| 5 |
∵直线kx+y+4=0，
∴
| 5 |
| 5 | ||
|
所求直线的斜率为：±2．
故答案为：±2
点评：本题的考点是直线与圆的位置关系，主要涉及了构造四边形及其面积的求法，解题的关键是“若四边形面积最小，则圆心与点P的距离最小时，即距离为圆心到直线的距离时，切线长PA，PB最小”属于中档题．
练习册系列答案
相关题目
已知cos（60°+α）=
，且α为第三象限角，则cos（30°-α）+sin（30°-α）的值为（ ）
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
命题“若函数f（x）=logax（a＞0，a≠1）在其定义域内是减函数，则loga2＜0”的逆否命题是（ ）
| A、若loga2＜0，则函数f（x）=logax（a＞0，a≠1）在其定义域内不是减函数 |
| B、若loga2≥0，则函数f（x）=logax（a＞0，a≠1）在其定义域内不是减函数 |
| C、若loga2＜0，则函数f（x）=logax（a＞0，a≠1）在其定义域内是减函数 |
| D、若loga2≥0，则函数f（x）=logax（a＞0，a≠1）在其定义域内是减函数 |
已知x，y是两个具有线性相关关系的变量，现有这两个变量的十个样本点（x1，y1）（x2，y2），…，（x10，y10），同学甲利用最小二乘法得到回归直线l1：y=bx+a，同学乙将十个样本点中的两个点连起来得到拟合直线l2：y=dx+c，则下列判断一定正确的是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
