题目内容
6个考题中3道难题,甲、乙、丙三人依次抽题(不放回),每次限抽一题,求甲、乙、丙三人各自抽中难题的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:分别计算出6个考题甲、乙、丙三人每人抽取两道的取法总数,和甲、乙、丙三人各自抽中难题的取法种数,代入古典概型概率计算公式,可得答案.
解答:
解:6个考题甲、乙、丙三人每人抽取两道共有:
•
•
=90种不同情况,
其中甲、乙、丙三人各自抽中难题有:
•
=36种情况,
故甲、乙、丙三人各自抽中难题的概率P=
=
| C | 2 6 |
| C | 2 4 |
| C | 2 2 |
其中甲、乙、丙三人各自抽中难题有:
| A | 3 3 |
| A | 3 3 |
故甲、乙、丙三人各自抽中难题的概率P=
| 36 |
| 90 |
| 2 |
| 5 |
点评:本题主要考查古典概率模型的概率公式,即如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法正确的是( )
A、当x=
| ||||||
B、当x=
| ||||||
| C、因为sin(π-x)=sinx,所以π是y=sinx的一个周期 | ||||||
D、因为cos(
|
函数y=sin(-
+
)的最小正周期为( )
| x |
| 2 |
| π |
| 4 |
| A、π | ||
| B、2π | ||
| C、4π | ||
D、
|
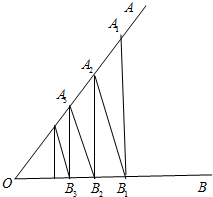 如图,相交于点O的两条直线OA,OB,在OA上取一点A,作A1B1⊥OB,作B1A2⊥OA,作A2B2⊥OB…一直无限地作下去,若已知A1B1=7,B1A2=6,则所有垂线长度的和等于
如图,相交于点O的两条直线OA,OB,在OA上取一点A,作A1B1⊥OB,作B1A2⊥OA,作A2B2⊥OB…一直无限地作下去,若已知A1B1=7,B1A2=6,则所有垂线长度的和等于