题目内容
已知函数f(x)=(2cos2x-1)cosφ+sin2xsinφ(0<φ<π)的图象过点(
,1).
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)将函数f(x)的图象上所有点的横坐标缩短到原来的
倍,纵坐标不变,得到函数g(x)的图象,求函数g(x)的单调递减区间.
| π |
| 12 |
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)将函数f(x)的图象上所有点的横坐标缩短到原来的
| 1 |
| 2 |
考点:三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的求值,三角函数的图像与性质
分析:(Ⅰ)利用两角和公式对函数解析式化简整理,把点的坐标代入求得φ,得到函数解析式.
(Ⅱ)利用图象变换的性质,求得g(x)的解析式,进而利用三角函数的图象和性质求得其单调递减区间.
(Ⅱ)利用图象变换的性质,求得g(x)的解析式,进而利用三角函数的图象和性质求得其单调递减区间.
解答:
解:(I)f(x)=(2cos2x-1)cosφ+sin2xsinφ=cos2xcosφ+sin2xsinφ=cos(2x-φ),
∵f(x)图象过点(
,1)
∴f(
)=cos(
-φ)=1,
∵0<φ<π,
∴-
<
-φ<
,
∴
-φ=0即φ=
.
∴f(x)=cos(2x-
).
(II)依题意可得g(x)=cos(4x-
),
当2kπ≤4x-
≤2kπ+π(k∈Z)时,即
+
≤x≤
+
(k∈Z)时,函数单调减,
∴g(x)的单调递减区间为[
+
,
+
](k∈Z).
∵f(x)图象过点(
| π |
| 12 |
∴f(
| π |
| 12 |
| π |
| 6 |
∵0<φ<π,
∴-
| 5π |
| 6 |
| π |
| 6 |
| π |
| 6 |
∴
| π |
| 6 |
| π |
| 6 |
∴f(x)=cos(2x-
| π |
| 6 |
(II)依题意可得g(x)=cos(4x-
| π |
| 6 |
当2kπ≤4x-
| π |
| 6 |
| kπ |
| 2 |
| π |
| 24 |
| kπ |
| 2 |
| 7π |
| 24 |
∴g(x)的单调递减区间为[
| kπ |
| 2 |
| π |
| 24 |
| kπ |
| 2 |
| 7π |
| 24 |
点评:本题主要考查三角恒等变换,三角函数的图象与性质等基础知识;考查运算求解能力,考查函数方程思想、数形结合思想.

练习册系列答案
相关题目
等比数列{an]中,“a1<a3”是“a4<a6”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
当实数x,y满足不等式
时,恒有ax+y≤2成立,则实数a的取值集合是( )
|
| A、(0,1] |
| B、(-∞,1] |
| C、(-1,1] |
| D、(1,2) |
已知集合A={-1,0,1},B={x|x+1>0},那么A∩B等于( )
| A、{0,1} |
| B、{-1,0,1} |
| C、(-1,+∞) |
| D、[-1,+∞) |
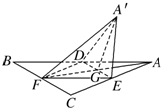 如图,正三角形ABC的中线AF与中位线DE相交于点G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列四个命题:
如图,正三角形ABC的中线AF与中位线DE相交于点G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列四个命题: