题目内容
已知(2x+
)n展开式前两项的二项式系数的和为10.
(1)求n的值.
(2)求出这个展开式中的常数项.
| 1 | ||
|
(1)求n的值.
(2)求出这个展开式中的常数项.
考点:二项式系数的性质
专题:排列组合
分析:(1)根据二项式展开式得到前两项的系数,根据系数和解的n的值,
(2)利用展开式的通项,求常数项,只要使x的次数为0即可.
(2)利用展开式的通项,求常数项,只要使x的次数为0即可.
解答:
解:(1)∵(2x+
)n展开式前两项的二项式系数的和为10
∴
+
=10,解得n=9;
(2)∵(2x+
)n展开式的通项Tr+1=
(2x)n-r(
)r=2n-r
xn-
----8分
∴令n-
=0且n=9得r=6,
∴(2x+
)n展开式中的常数项为第7项,即T7=29-6•
=672.
| 1 | ||
|
∴
| C | 0 n |
| C | 1 n |
(2)∵(2x+
| 1 | ||
|
| C | r n |
| 1 | ||
|
| C | r n |
| 3r |
| 2 |
∴令n-
| 3r |
| 2 |
∴(2x+
| 1 | ||
|
| C | 6 9 |
点评:本题主要考查了二项式定理,利用好通项,属于基础题.

练习册系列答案
相关题目
执行如图的程序框图,则输出的M是( )
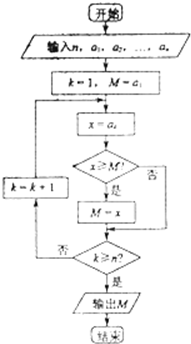

| A、a1,a2,…,an的平均数 |
| B、a1,a2,…,an的中位数 |
| C、a1,a2,…,an中的最大数 |
| D、a1,a2,…,an中的最小数 |
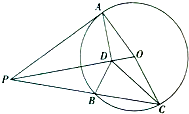 如图,AP是圆O的切线,A是切点,AD⊥OP与D点,过点P作圆O的割线与圆O相交于B,C两点
如图,AP是圆O的切线,A是切点,AD⊥OP与D点,过点P作圆O的割线与圆O相交于B,C两点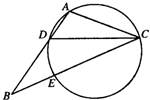 如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC
如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC