题目内容
已知二次函数f(x)=x2+bx+c,且f(x)+4=0的解集为{x|x=1}
(1)求函数f(x)的解析式;
(2)若函数f(x)在区间[a,a+4]上存在零点,求a的取值范围.
(1)求函数f(x)的解析式;
(2)若函数f(x)在区间[a,a+4]上存在零点,求a的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)中由题意读出二次函数的顶点坐标,代入顶点坐标公式求出b,c的值,从而求出二次函数表达式;(2)中找出零点,解不等式组,求出a的范围.
解答:
解:(1)由f(x)+4=0的解集为{x|x=1},
∴f(x)的顶点坐标为:(1,-4),
∴
,
解得:b=-2,c=-3.
∴f(x)=x2-2x-3,
(2)由(1)得函数与x轴的交点为(-1,0),(3,0),
∴
,
解得:-5≤a≤3.
∴a的取值范围是:[-5,3].
∴f(x)的顶点坐标为:(1,-4),
∴
|
解得:b=-2,c=-3.
∴f(x)=x2-2x-3,
(2)由(1)得函数与x轴的交点为(-1,0),(3,0),
∴
|
解得:-5≤a≤3.
∴a的取值范围是:[-5,3].
点评:本题考察了二次函数的性质,顶点坐标公式,函数的零点,是一道中档题.

练习册系列答案
相关题目
定义域为R的函数y=f(x)的值域为[a,b],则函数y=f(x+c)的值域为( )
| A、[a+c,b+c] |
| B、[a-c,b-c] |
| C、[a,b] |
| D、不确定 |
 某企业生产一种汽车配件,经抽样统计,该企业生产的配件尺寸的样本频率分布直方图如下.配件尺寸在[60,62)内的为一等品,尺寸在[58,60)或[62,64)内的为二等品,其余为三等品.用频率近似表示概率.
某企业生产一种汽车配件,经抽样统计,该企业生产的配件尺寸的样本频率分布直方图如下.配件尺寸在[60,62)内的为一等品,尺寸在[58,60)或[62,64)内的为二等品,其余为三等品.用频率近似表示概率.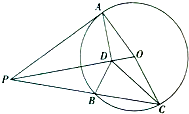 如图,AP是圆O的切线,A是切点,AD⊥OP与D点,过点P作圆O的割线与圆O相交于B,C两点
如图,AP是圆O的切线,A是切点,AD⊥OP与D点,过点P作圆O的割线与圆O相交于B,C两点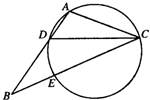 如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC
如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC 如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有
如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有