题目内容
13．函数f（x）=ex（x-aex） 恰有两个极值点x1，x2（x1＜x2），则a的取值范围是（0，$\frac{1}{2}$）．分析 根据题意，对函数f（x）求导数，得出导数f′（x）=0有两不等实根，转化为两函数有两个交点的问题，结合图象即可得出a的取值范围．
解答 解：∵函数f（x）=ex（x-aex），求导，f′（x）=（x+1-2a•ex）ex，
由于函数f（x）的两个极值点为x1，x2，
即x1，x2是方程f′（x）=0的两不等实根，
即方程x+1-2aex=0，且a≠0，$\frac{x+1}{2a}$=ex；
设y1=$\frac{x+1}{2a}$（a≠0），y2=ex，
在同一坐标系内画出这两个函数的图象，
如图所示：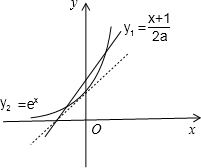
要使这两个函数有2个不同的交点，应满足$\left\{\begin{array}{l}{\frac{1}{2a}＞0}\\{\frac{1}{2a}＞1}\end{array}\right.$，
解得：0＜a＜$\frac{1}{2}$，
∴a的取值范围是（0，$\frac{1}{2}$），
故答案为：（0，$\frac{1}{2}$）．
点评 本题考查利用导数研究函数的单调性与极值的应用，也考查了转化思想与数形结合的应用问题，是综合性题目，属于中档题．
练习册系列答案
相关题目
3．已知函数$f（x）=\left\{\begin{array}{l}lnx，x＞0\\-x，x＜0\end{array}\right.$，若$f（{\frac{1}{3}}）=\frac{1}{3}f（a）$，则实数a的值为（ ）
| A． | $\frac{1}{27}$ | B． | $-\frac{1}{27}$ | C． | ln27 | D． | $ln\frac{1}{27}$ |
8．复数$\frac{5}{2-i}$的虚部是（ ）
| A． | i | B． | -i | C． | 1 | D． | -1 |
5．已知复数$z=\frac{5a}{2+i}+\frac{1+i}{1-i}，a∈R$，若复数z对应的点在复平面内位于第四象限，则实数a的取值范围是（ ）
| A． | a＞1 | B． | a＜0 | C． | 0＜a＜1 | D． | a＜1 |
3．国家标准规定：轻型汽车的氮氧化物排放量不得超过80mg/km．根据这个标准，检测单位从某出租车公司运营的A、B两种型号的出租车中分别抽取5辆，对其氮氧化物的排放量进行检测，检测结果记录如下（单位：mg/km）
（Ⅰ）从被检测的5辆A型号的出租车和5辆B型号的出租车中分别抽取2辆，求抽取的这4辆车的氮氧化物排放量均不超过80mg/km的概率；
（Ⅱ）从被检测的5辆B种型号的出租车中任取2辆，记“氮氧化物排放量超过80mg/km”的车辆数为ξ，求ξ的分布列．
| A | 85 | 80 | 85 | 60 | 90 |
| B | 70 | 90 | 95 | 70 | 75 |
（Ⅱ）从被检测的5辆B种型号的出租车中任取2辆，记“氮氧化物排放量超过80mg/km”的车辆数为ξ，求ξ的分布列．
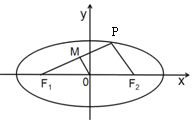已知P为椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上任意一点，F1，F2为左、右焦点，M为PF1中点．如图所示：若|OM|+$\frac{1}{2}$|PF1|=2，离心率e=$\frac{\sqrt{3}}{2}$．