题目内容
14.已知点P(2,2),圆C:x2+y2-8y=0,过点P的动直线l与圆C交于A,B两点,线段AB的中点为M,O为坐标原点.当|OP|=|OM|时,则直线l的斜率( )| A. | k=3 | B. | k=-3 | C. | k=$\frac{1}{3}$ | D. | k=-$\frac{1}{3}$ |
分析 圆心为C(0,4),半径为4.设M(x,y),则$\overrightarrow{CM}$=(x,y-4),$\overrightarrow{MP}$=(2-x,2-y).由题设知$\overrightarrow{CM}$•$\overrightarrow{MP}$=0,从而M的轨迹方程是(x-1)2+(y-3)2=2.当|OP|=|OM|时,x2+y2=8,由P在以(1,3)为圆心,$\sqrt{2}$为半径的圆上,知|CP|=|CM|,由此能求出直线l的斜率.
解答 解:圆C的方程可化为x2+(y-4)2=16,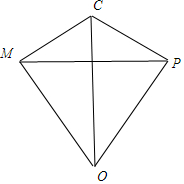
所以圆心为C(0,4),半径为4.
设M(x,y),则$\overrightarrow{CM}$=(x,y-4),$\overrightarrow{MP}$=(2-x,2-y).
由题设知$\overrightarrow{CM}$•$\overrightarrow{MP}$=0,
故x(2-x)+(y-4)(2-y)=0,即(x-1)2+(y-3)2=2.
由于点P在圆C的内部,所以M的轨迹方程是(x-1)2+(y-3)2=2.
当|OP|=|OM|时,x2+y2=8,
∵P(2,2)满足M的轨迹方程,即P在以(1,3)为圆心,$\sqrt{2}$为半径的圆上,
∴|CP|=|CM|,
∴直线l的斜率kPM=-$\frac{1}{{k}_{OC}}$=-$\frac{1}{3}$.
故选:D.
点评 本题考查直线的斜率的求法,考查圆的方程、直线与圆的位置关系,考查推理论证能力、运算求解能力,考查转化化归思想、数形结合思想,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.在直角△ABC中,∠BCA=90°,CA=CB=1,P为AB边上的点$\overrightarrow{AP}$=λ$\overrightarrow{AB}$,若$\overrightarrow{CP}$•$\overrightarrow{AB}$≥$\overrightarrow{PA}$•$\overrightarrow{PB}$,则λ的最大值是( )
| A. | $\frac{{2+\sqrt{2}}}{2}$ | B. | $\frac{{2-\sqrt{2}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
3.已知函数f(x)=2x+2,则f(2)的值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
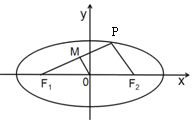 已知P为椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上任意一点,F1,F2为左、右焦点,M为PF1中点.如图所示:若|OM|+$\frac{1}{2}$|PF1|=2,离心率e=$\frac{\sqrt{3}}{2}$.
已知P为椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上任意一点,F1,F2为左、右焦点,M为PF1中点.如图所示:若|OM|+$\frac{1}{2}$|PF1|=2,离心率e=$\frac{\sqrt{3}}{2}$.