题目内容
6.已知△ABC的内角A,B,C的对边分别为a,b,c,a2+b2=λab.(1)若$λ=\sqrt{6}$,$B=\frac{5π}{6}$,求sinA;
(2)若λ=4,AB边上的高为$\frac{{\sqrt{3}c}}{6}$,求C.
分析 (1)由已知结合正弦定理得:$4{sin^2}A-2\sqrt{6}sinA+1=0$,结合范围可求$sinA<\frac{1}{2}$,即可得解sinA的值.
(2)由题意及三角形面积公式可求${S_{△ABC}}=\frac{1}{2}absinC=\frac{{\sqrt{3}}}{12}{c^2}$,由余弦定理,三角函数恒等变换的应用化简可得$sin({C+\frac{π}{6}})=1$,结合范围$\frac{π}{6}<C+\frac{π}{6}<\frac{7π}{6}$,可求C的值.
解答 解:(1)由已知$B=\frac{5π}{6}$,${a^2}+{b^2}=\sqrt{6}ab$,结合正弦定理得:$4{sin^2}A-2\sqrt{6}sinA+1=0$,
于是$sinA=\frac{{\sqrt{6}±\sqrt{2}}}{4}$.
因为$0<A<\frac{π}{6}$,
所以$sinA<\frac{1}{2}$,
可得$sinA=\frac{{\sqrt{6}-\sqrt{2}}}{4}$.
(2)由题意可知${S_{△ABC}}=\frac{1}{2}absinC=\frac{{\sqrt{3}}}{12}{c^2}$,得:$\frac{1}{2}absinC=\frac{{\sqrt{3}}}{12}({{a^2}+{b^2}-2abcosC})=\frac{{\sqrt{3}}}{12}({4ab-2abcosC})$.
从而有:$\sqrt{3}sinC+cosC=2$,即$sin({C+\frac{π}{6}})=1$,
又因为$\frac{π}{6}<C+\frac{π}{6}<\frac{7π}{6}$,
所以,$C=\frac{π}{3}$.
点评 本题主要考查了正弦定理,三角形面积公式,余弦定理,三角函数恒等变换的应用,正弦函数的图象和性质的综合应用,考查了计算能力和转化思想,属于中档题.

| A. | 三角形 | B. | 长方形 | ||
| C. | 对角线不相等的菱形 | D. | 六边形 |
| A. | 3+4i | B. | 3-4i | C. | 5-4i | D. | 5+4i |
| A. | 1 | B. | 0 | C. | -2 | D. | 4 |
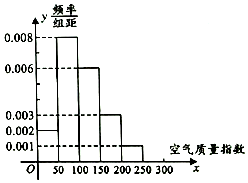 空气质量按照空气质量指数大小分为七档(五级),相对应空气质量的七个类别,指数越大,说明污染的情况越严重,对人体危害越大.
空气质量按照空气质量指数大小分为七档(五级),相对应空气质量的七个类别,指数越大,说明污染的情况越严重,对人体危害越大.| 指数 | 级别 | 类别 | 户外活动建议 |
| 0~50 | Ⅰ | 优 | 可正常活动 |
| 51~100 | Ⅱ | 良 | |
| 101~150 | Ⅲ | 轻微污染 | 易感人群症状有轻度加剧,健康人群出现刺激症状,心脏病和呼吸系统疾病患者应减少体积消耗和户外活动. |
| 151~200 | 轻度污染 | ||
| 201~250 | Ⅳ | 中度污染 | 心脏病和肺病患者症状显著加剧,运动耐受力降低,健康人群中普遍出现症状,老年人和心脏病、肺病患者应减少体力活动. |
| 251~300 | 中度重污染 | ||
| 301~500 | Ⅴ | 重污染 | 健康人运动耐受力降低,由明显强烈症状,提前出现某些疾病,老年人和病人应当留在室内,避免体力消耗,一般人群应尽量减少户外活动. |
(1)求这60天中属轻度污染的天数;
(2)求这60天空气质量指数的平均值;
(3)一般地,当空气质量为轻度污染或轻度污染以上时才会出现雾霾天气,且此时出现雾霾天气的概率为$\frac{5}{8}$,请根据统计数据,求在未来2天里,邵阳市恰有1天出现雾霾天气的概率.
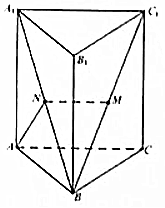 如图,直三棱柱ABC-A1B1C1中,AA1=AB,AB⊥BC,且N是A1B的中点.
如图,直三棱柱ABC-A1B1C1中,AA1=AB,AB⊥BC,且N是A1B的中点.