��Ŀ����
18��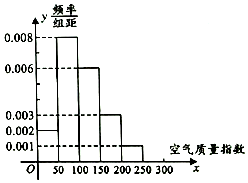 �����������տ�������ָ����С��Ϊ�ߵ����弶�������Ӧ�����������߸����ָ��Խ��˵����Ⱦ�����Խ���أ�������Σ��Խ��
�����������տ�������ָ����С��Ϊ�ߵ����弶�������Ӧ�����������߸����ָ��Խ��˵����Ⱦ�����Խ���أ�������Σ��Խ��| ָ�� | ���� | ��� | �������� |
| 0��50 | �� | �� | ������� |
| 51��100 | �� | �� | |
| 101��150 | �� | ����Ⱦ | ����Ⱥ֢״����ȼӾ磬������Ⱥ���ִ̼�֢״�����ಡ�ͺ���ϵͳ��������Ӧ����������ĺͻ����� |
| 151��200 | �����Ⱦ | ||
| 201��250 | �� | �ж���Ⱦ | ���ಡ�ͷβ�����֢״�����Ӿ磬�˶����������ͣ�������Ⱥ���ձ����֢״�������˺����ಡ���β�����Ӧ����������� |
| 251��300 | �ж�����Ⱦ | ||
| 301��500 | �� | ����Ⱦ | �������˶����������ͣ�������ǿ��֢״����ǰ����ijЩ�����������˺Ͳ���Ӧ���������ڣ������������ģ�һ����ȺӦ�������ٻ����� |
��1������60�����������Ⱦ��������
��2������60���������ָ����ƽ��ֵ��
��3��һ��أ�����������Ϊ�����Ⱦ�������Ⱦ����ʱ�Ż���������������Ҵ�ʱ�������������ĸ���Ϊ$\frac{5}{8}$�������ͳ�����ݣ�����δ��2���������ǡ��1��������������ĸ��ʣ�
���� ��1����2������Ƶ�ʷֲ�ֱ��ͼ�����㼴�ɣ�
��3�������������Ϊ�����Ⱦ�������Ⱦ���ϵĸ���P1���õ������������ʣ��Ӷ����������ǡ��1��������������ĸ��ʣ�
��� �⣺��1��������֪�������Ⱦ����������ָ����151-200֮�䣬����0.003��50��60=9�죮
��2����ֱ��ͼ֪60���������ָ����ƽ��ֵΪ$\overline x=25��0.1+75��0.4+125��0.3+175��0.15+225��0.05=107.5$��
��3����������Ϊ�����Ⱦ�������Ⱦ���ϵĸ���P1=0.15+0.05=0.2��
�������������Ϊ$0.2��\frac{5}{8}=\frac{1}{8}$��
��δ��2���ǡ��1��Ϊ���������ĸ���$P=C_2^1��{��\frac{1}{8}��^1}��{��1-\frac{1}{8}��^1}=\frac{7}{32}$��
���� ���⿼����Ƶ�ʷֲ�ֱ��ͼ��Ӧ�����⣬Ҳ������������¼��ĸ��ʵļ������⣬���е��⣮

��ϰ��ϵ�д�
 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�
�����Ŀ
13��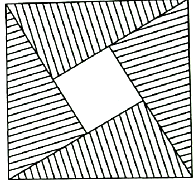 ��ͼ��ʾ����Ӱ���������ĸ�ȫ�ȵ�ֱ����������ɵ�ͼ�Σ��ڴ������������ȡһ�㣬��һ������С�����εĸ���Ϊ$\frac{1}{5}$����ֱ���������нϴ�����Ϊ�ȣ���sin��=��������
��ͼ��ʾ����Ӱ���������ĸ�ȫ�ȵ�ֱ����������ɵ�ͼ�Σ��ڴ������������ȡһ�㣬��һ������С�����εĸ���Ϊ$\frac{1}{5}$����ֱ���������нϴ�����Ϊ�ȣ���sin��=��������
 ��ͼ��ʾ����Ӱ���������ĸ�ȫ�ȵ�ֱ����������ɵ�ͼ�Σ��ڴ������������ȡһ�㣬��һ������С�����εĸ���Ϊ$\frac{1}{5}$����ֱ���������нϴ�����Ϊ�ȣ���sin��=��������
��ͼ��ʾ����Ӱ���������ĸ�ȫ�ȵ�ֱ����������ɵ�ͼ�Σ��ڴ������������ȡһ�㣬��һ������С�����εĸ���Ϊ$\frac{1}{5}$����ֱ���������нϴ�����Ϊ�ȣ���sin��=��������| A�� | $\frac{{\sqrt{5}}}{5}$ | B�� | $\frac{{2\sqrt{5}}}{5}$ | C�� | $\frac{{\sqrt{3}}}{3}$ | D�� | $\frac{{\sqrt{2}}}{2}$ |
3����֪����A={x|x2-2x��0}��$B=\left\{{x\left|{-\sqrt{3}��x��\sqrt{3}}\right.}\right\}$����A��B=��������
| A�� | $\left\{{x\left|{-\sqrt{3}��x��0}\right.}\right\}$ | B�� | $\left\{{x\left|{-\sqrt{3}��x��2}\right.}\right\}$ | C�� | $\left\{{x\left|{0��x��\sqrt{3}}\right.}\right\}$ | D�� | {x|-2��x��0} |
1����x��0��y��0��������ʽ2log${\;}_{\frac{1}{2}}$[��a-1��x+ay]��1+log${\;}_{\frac{1}{2}}$��xy�����������4a����СֵΪ��������
| A�� | $\frac{\sqrt{6}+2}{4}$ | B�� | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C�� | $\sqrt{6}$+2 | D�� | $\sqrt{6}$+$\sqrt{2}$ |