题目内容

已知函数f（x+1）=3x+2，则f（x）的解析式是（　　）
A、f（x）=3x+2
B、f（x）=3x+1
C、f（x）=3x-1
D、f（x）=3x+4
考点：函数解析式的求解及常用方法
专题：计算题
分析：换元法整体代入求解．
解答： 解：设t=x+1，
∵函数f（x+1）=3x+2=3（x+1）-1
∴函数f（t）=3t-1，
即函数f（x）=3x-1
故选：C
点评：本题考查了函数解析式的求解，很容易．
练习册系列答案
相关题目
曲线C上的动点P到点M（2，
15
4
）和到y=
17
4
的距离相等，
（1）求曲线的解析式；
（2）设P是曲线C在区间[0，4]上任一点，A、B两点坐标分别为A（0，0）、B（4，0），求
PA
•
PB
取值范围；
（3）P（x0，y0）是曲线上任一点，若曲线l与C有且仅有一个公共点恰为P，当1≤x0≤6时，求l在x轴上截距的取值范围．
已知函数f（x）=x2+2ax+2在[-5，5]上单调，则实数a的取值范围是（　　）
A、（-∞，-5]
B、[5，+∞）
C、[-5，5]
D、（-∞，-5]∪[5，+∞）
圆C：x2+y2-4x+4
3
y=0的圆心到直线x+
3
y=0的距离是
 
．
若x，y满足
x+y-2≤0
2x-y+2≥0
y≥0
，则z=y-x的最大值为（　　）
A、2B、-2C、1D、-1
现有四个函数：①y=x•sinx；②y=x•cosx；③y=x•|cosx|；④y=x•2x的图象（部分）如下：

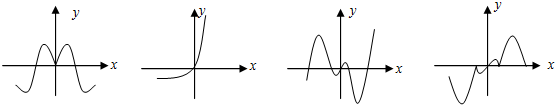
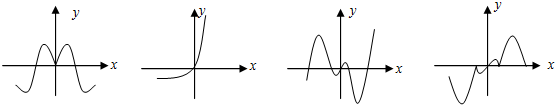
则按照从左到右图象对应的函数序号安排正确的一组是（　　）
A、①④③②B、③④②①
C、④①②③D、①④②③
（1）已知二次函数f（x）满足条件f（0）=1及f（x+1）-f（x）=2x，求f（x）．
（2）若f（x）满足关系式f（x）+2f（
1
x
）=3x，求f（x）．
函数y=ax2+1（a＜0，-1≤x≤2）的单调递减区间为
 
．
已知函数f（x）=ax-1的图象经过（5，
1
6
），其中a＞0且a≠1，求函数g（x）=a2x-ax-2+8，x∈（-2，1）的值域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网