题目内容
1.△ABC的内角A,B,C的对边分别为a,b,c,已知sinA+sinC=2sinB,b=2,ac=b2,试判断三角形形状.分析 利用正弦定理,结合条件,即可判断三角形形状.
解答 解:∵sinA+sinC=2sinB,b=2,ac=b2,
∴a+c=4,ac=4
∴a=c=2,
∴a=b=c,
∴△ABC是等边三角形.
点评 本题考查判断三角形形状,考查了正弦定理的应用,属于基本知识的考查.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
11.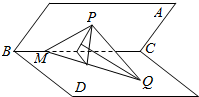 如图所示,二面角A-BC-D的大小为45°,P为平面ABC内一点,Q为平面BCD内一点,M为BC上一点,已知P在平面BCD内的射影恰好在线段MQ上,设PM=$\sqrt{2}$,∠CMQ=45°,直线PQ与平面BCD所成的角为30°,则PQ的长为( )
如图所示,二面角A-BC-D的大小为45°,P为平面ABC内一点,Q为平面BCD内一点,M为BC上一点,已知P在平面BCD内的射影恰好在线段MQ上,设PM=$\sqrt{2}$,∠CMQ=45°,直线PQ与平面BCD所成的角为30°,则PQ的长为( )
 如图所示,二面角A-BC-D的大小为45°,P为平面ABC内一点,Q为平面BCD内一点,M为BC上一点,已知P在平面BCD内的射影恰好在线段MQ上,设PM=$\sqrt{2}$,∠CMQ=45°,直线PQ与平面BCD所成的角为30°,则PQ的长为( )
如图所示,二面角A-BC-D的大小为45°,P为平面ABC内一点,Q为平面BCD内一点,M为BC上一点,已知P在平面BCD内的射影恰好在线段MQ上,设PM=$\sqrt{2}$,∠CMQ=45°,直线PQ与平面BCD所成的角为30°,则PQ的长为( )| A. | $\frac{2}{3}\sqrt{6}$ | B. | $\frac{3}{4}\sqrt{6}$ | C. | $\frac{4}{3}\sqrt{2}$ | D. | $\frac{3}{2}\sqrt{2}$ |
13.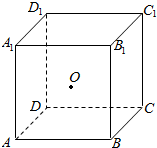 正方体ABCD-A1B1C1D1边长为2,O为正方体的中心,动点P在正方体底面ABCD内运动(包括边界),若AO⊥OP,则点P的轨迹为( )
正方体ABCD-A1B1C1D1边长为2,O为正方体的中心,动点P在正方体底面ABCD内运动(包括边界),若AO⊥OP,则点P的轨迹为( )
 正方体ABCD-A1B1C1D1边长为2,O为正方体的中心,动点P在正方体底面ABCD内运动(包括边界),若AO⊥OP,则点P的轨迹为( )
正方体ABCD-A1B1C1D1边长为2,O为正方体的中心,动点P在正方体底面ABCD内运动(包括边界),若AO⊥OP,则点P的轨迹为( )| A. | 椭圆的一部分 | B. | 线段 | C. | 圆的部分 | D. | 抛物线的一部分 |
10.在△ABC中,tanA+tanB+$\sqrt{3}$=$\sqrt{3}$tanAtanB,且sinA•cosA=$\frac{\sqrt{3}}{4}$,则此三角形为( )
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
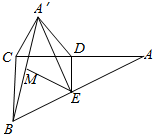 已知在△ABC中,D,E分别为AC,AB的中点,沿DE将△ADE折起,使A到A′的位置,若M是A′B的中点,求证:ME∥平面A′CD.
已知在△ABC中,D,E分别为AC,AB的中点,沿DE将△ADE折起,使A到A′的位置,若M是A′B的中点,求证:ME∥平面A′CD. 如图,ABCD是边长为2的正方形,ED=1,DE⊥平面ABCD,EF∥BD,且EF=$\frac{1}{2}$BD.
如图,ABCD是边长为2的正方形,ED=1,DE⊥平面ABCD,EF∥BD,且EF=$\frac{1}{2}$BD.