Question

【题目】选修4-4：坐标系与参数方程

已知在极坐标系和直角坐标系中，极点与直角坐标系的原点重合，极轴与轴的非负半轴重合，曲线的极坐标方程为，曲线的参数方程为（为参数）.

（1）求曲线的直角坐标方程和曲线的普通方程；

（2）判断曲线与曲线的位置关系，若两曲线相交，求出两交点间的距离.

Answer 1

【答案】(1) (2)

【解析】试题分析：（1）曲线的极坐标方程为，即，利用，即可化为直角坐标方程，曲线的参数方程为（为参数），消去即可化为普通方程；（2）由（1）知曲线和曲线都是圆，将两圆方程相减即可得两圆公共弦所在的直线方程，即可求出两交点间的距离.

试题解析：（1）∵

∴，

将代入上式整理得曲线的直角坐标方程为，

由为参数）消去参数得曲线的普通方程为.

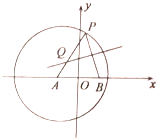
（2）由（1）知曲线是圆心为（1,0），半径的圆，

曲线是圆心为（0,1），半径=2的圆，

∵，∴两圆相交，

两圆方程相减得公共弦所在的直线方程为，

∴圆心到公共弦所在直线的距离为=，

∴公共弦长为=.