题目内容
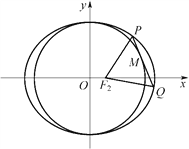
【题目】如图,点![]() 是圆
是圆![]() 内的一个定点,点
内的一个定点,点![]() 是圆
是圆![]() 上的任意一点,线段
上的任意一点,线段![]() 的垂直平分线
的垂直平分线![]() 和半径
和半径![]() 相交于点
相交于点![]() ,当点
,当点![]() 在圆
在圆![]() 上运动时,点
上运动时,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
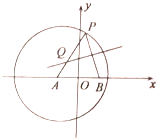
(1)求曲线![]() 的方程;
的方程;
(2)点![]() ,
, ![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的值.
的值.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:
本题考查曲线方程的求法和直线与圆锥曲线的位置关系.(1)由条件根据定义法求解曲线方程.(2)设出直线![]() 的方程,然后根据根与系数的关系求得点
的方程,然后根据根与系数的关系求得点![]() 的坐标.由点
的坐标.由点![]() ,
, ![]() ,
, ![]() 共线可得点
共线可得点![]() 的横坐标
的横坐标![]() ,可得直线
,可得直线![]() 与
与![]() 轴的交点纵坐标为
轴的交点纵坐标为![]() ,由此可得
,由此可得![]() ,
, ![]() ,计算后可得结果.
,计算后可得结果.
试题解析:
(1)由题意得点![]() 在
在![]() 的垂直平分线上,
的垂直平分线上,
所以![]() ,
,
∴![]() .
.
∴点![]() 的轨迹是以
的轨迹是以![]() 为焦点,长轴长为4的椭圆,
为焦点,长轴长为4的椭圆,
设椭圆的方程为![]() ,
,
则![]() ,
, ![]() ,
,
∴![]() .
.
所以曲线![]() 的方程为
的方程为![]() .
.
(2)由题设知直线的斜率存在.设直线![]() 的方程为
的方程为![]() ,
,
由 消去
消去![]() 整理得
整理得
![]() ,
,
设![]() ,
, ![]() ,
,
则![]() ,
,
又![]() ,
,
所以![]() ,
,
所以 ,
,
因为点![]() ,
, ![]() ,
, ![]() 共线,故
共线,故![]() ,
,
即 ,
,
所以![]() ,
,
又直线![]() 与
与![]() 轴的交点纵坐标为
轴的交点纵坐标为![]() ,
,
所以![]() ,
, ![]() ,
,
所以![]() .
.

练习册系列答案
相关题目