题目内容
8. 已知△ABD和△BCD是两个直角三角形,∠BAD=∠BDC=$\frac{π}{2}$,E、F分别是边AB、AD的中点,现将△ABD沿BD边折起到A1BD的位置,如图所示,使平面A1BD⊥平面BCD.
已知△ABD和△BCD是两个直角三角形,∠BAD=∠BDC=$\frac{π}{2}$,E、F分别是边AB、AD的中点,现将△ABD沿BD边折起到A1BD的位置,如图所示,使平面A1BD⊥平面BCD.(Ⅰ)求证:EF∥平面BCD;
(Ⅱ)求证:平面A1BC⊥平QUOTE A1BC⊥面A1CD;
(Ⅲ)请你判断,A1C与BD是否有可能垂直,做出判断并写明理由.
分析 (Ⅰ)证明:EF∥BD,即可证明EF∥平面BCD;
(Ⅱ)证明A1B⊥平面A1CD,即可证明平面A1BC⊥平面A1CD;
(Ⅲ)利用反证法进行证明.
解答 (Ⅰ)证明:因为E、F分别是边AB、AD的中点,
所以EF∥BD,
因为EF?平面BCD,BD?平面BCD,
所以EF∥平面BCD.------------(4分)
(Ⅱ)证明:因为平面A1BD⊥平面BCD,平面A1BD∩平面BCD=BD,
CD?平面BCD,CD⊥BD,所以CD⊥平面A1BD.
因为A1B?平面A1BD,
所以CD⊥A1B,
因为A1B⊥A1D,A1D∩CD=D,
所以A1B⊥平面A1CD.
因为A1B?平面A1BC,
所以平面A1BC⊥平面A1CD.------------(10分)
(Ⅲ)结论:A1C 与BD 不可能垂直.
理由如下:
假设A1C⊥BD,
因为CD⊥BD,A1C∩CD=C,
所以BD⊥平面A1CD,
因为A1D⊥平面A1CD,
所以BD⊥A1D与 A1B⊥A1D矛盾,故A1C 与不可能垂直.----------------(13分)
点评 本题考查线面平行、面面垂直的判定,考查反证法的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
16.已知函数$f(x)=cosx+{2^x}-\frac{1}{2}(x<0)$与g(x)=cosx+log2(x+a)图象上存在关于y轴对称的点,则a的取值范围是( )
| A. | $(-∞,-\sqrt{2})$ | B. | $(-∞,-\frac{{\sqrt{2}}}{2})$ | C. | $(-\sqrt{2},\frac{{\sqrt{2}}}{2})$ | D. | $(-∞,\sqrt{2})$ |
20.圆心在直线2x-y-6=0上的圆C与y轴交于两点A(0,-5),B(0,-3),则圆C的方程是( )
| A. | (x-1)2+(y+4)2=2 | B. | (x+1)2+(y-4)2=2 | C. | (x-1)2+(y-4)2=2 | D. | (x+1)2+(y+4)2=2 |
17.已知抛物线x2=2px(p>0)经过点线$M({\frac{1}{2},2})$,则它的准线方程为( )
| A. | $y=-\frac{1}{32}$ | B. | B | C. | C | D. | D |
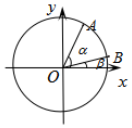 如图,在平面直角坐标系xOy中,以x轴为始边作两个锐角α,β,它们的终边分别与单位圆交于A,B两点.已知$A(\frac{{\sqrt{5}}}{5},\;\frac{{2\sqrt{5}}}{5})\;,\;\;B(\frac{{7\sqrt{2}}}{10},\;\frac{{\sqrt{2}}}{10})$
如图,在平面直角坐标系xOy中,以x轴为始边作两个锐角α,β,它们的终边分别与单位圆交于A,B两点.已知$A(\frac{{\sqrt{5}}}{5},\;\frac{{2\sqrt{5}}}{5})\;,\;\;B(\frac{{7\sqrt{2}}}{10},\;\frac{{\sqrt{2}}}{10})$ 已知函数$f(x)=2sin(2x+φ)\;(|φ|<\frac{π}{2})$部分图象如图所示.
已知函数$f(x)=2sin(2x+φ)\;(|φ|<\frac{π}{2})$部分图象如图所示.