题目内容
11.已知函数f(x)=ex(ax2-2x-2),a∈R且a≠0.(1)若曲线y=f(x)在点P(2,f(2))处的切线垂直于y轴,求实数a的值;
(2)在(1)的条件下,若y=kx与y=f(x)的图象存在三个交点,求k的取值范围.
分析 (1)欲求实数a的值,只须求出切线斜率的值列出关于a的等式即可,故先利用导数求出在x=2处的导函数值,再结合导数的几何意义即可求出切线的斜率,最后利用斜率为0即可求得a;
(2)欲使y=kx与y=f(x)的图象存在三个交点,只需kx=ex(x2-2x-2)有三解,将k分离,研究另一侧函数的图象性质,结合图象可求出k的取值范围.
解答  解:(1)f′(x)=(ex)′•(ax2-2x-2)+ex•(ax2-2x-2)′
解:(1)f′(x)=(ex)′•(ax2-2x-2)+ex•(ax2-2x-2)′
=ex•(ax2-2x-2)+ex•(2ax-2)
=a•ex•(x-$\frac{2}{a}$)(x+2).
∵曲线y=f(x)在点P(2,f(2))处的切线垂直于y轴,
由导数的几何意义得f′(2)=0,
∴a=1.
∴实数a的值为:1.
(2)∵y=kx与y=f(x)的图象存在三个交点
∴kx=ex(x2-2x-2)有三解,即k=$\frac{{e}^{x}({x}^{2}-2x-2)}{x}$
而令g(x)=$\frac{{e}^{x}({x}^{2}-2x-2)}{x}$则g′(x)=$\frac{{e}^{x}({x}^{3}-{x}^{2}-2x+2)}{{x}^{2}}$=$\frac{{e}^{x}(x-1)({x}^{2}-2)}{{x}^{2}}$.
令g′(x)=0解得x=1或$±\sqrt{2}$
当x<-$\sqrt{2}$时,g′(x)<0,当-2<x<0时,g′(x)>0,
当0<x<1时,g′(x)>0,当1<x<2时,g′(x)<0,当x>2时,g′(x)>0
∴当x=-$\sqrt{2}$时函数取极小值g(-2)=-3e-2,当x=1时,函数取极大值g(1)=-3e,
当x=2时,函数取极小值g(2)=-e2,画出函数图象
结合函数的图象可知-e2<k<-3e或-3e-2<k<0
点评 本题主要考查了利用导数研究曲线上某点切线方程,以及利用导数研究函数的极值,同时考查了转化的思想和运算求解的能力,属于难题.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案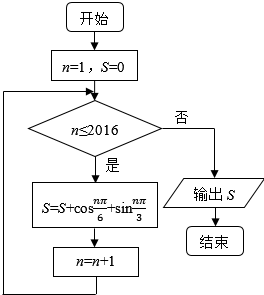 执行如图所示的程序框图,则输出结果S=( )
执行如图所示的程序框图,则输出结果S=( )| A. | 0 | B. | -1 | C. | $\frac{1-\sqrt{3}}{2}$ | D. | $\frac{1+\sqrt{3}}{2}$ |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |