题目内容
1.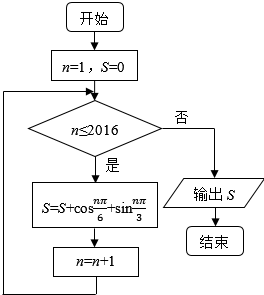 执行如图所示的程序框图,则输出结果S=( )
执行如图所示的程序框图,则输出结果S=( )| A. | 0 | B. | -1 | C. | $\frac{1-\sqrt{3}}{2}$ | D. | $\frac{1+\sqrt{3}}{2}$ |
分析 由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
解答 解:由已知可得该程序的功能是利用循环结构计算并输出变量S=$cos\frac{π}{6}+sin\frac{π}{3}$+$cos\frac{2π}{6}+sin\frac{2π}{3}$+$cos\frac{3π}{6}+sin\frac{3π}{3}$+…+$cos\frac{2016π}{6}+sin\frac{2016π}{3}$的值,
∵$cos\frac{2016π}{6}+sin\frac{2016π}{3}$的值以12为周期呈周期性变化,2016÷12=168,
故S=168($cos\frac{π}{6}+sin\frac{π}{3}$+$cos\frac{2π}{6}+sin\frac{2π}{3}$+$cos\frac{3π}{6}+sin\frac{3π}{3}$+…+$cos\frac{12π}{6}+sin\frac{12π}{3}$)=0,
故选:A
点评 本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答.

练习册系列答案
相关题目
12.已知i是虚数单位,$\frac{1-3i}{1-i}$=a+bi(a,b∈R),则a+b的值为( )
| A. | 3 | B. | 1 | C. | -1 | D. | -3 |
16.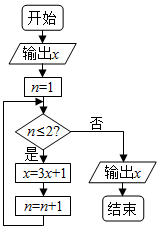 从1,2,3,4,5,6,7,8中随机取出一个数为x,执行如图所示的程序框图,则输出的x不小于40的概率为( )
从1,2,3,4,5,6,7,8中随机取出一个数为x,执行如图所示的程序框图,则输出的x不小于40的概率为( )
 从1,2,3,4,5,6,7,8中随机取出一个数为x,执行如图所示的程序框图,则输出的x不小于40的概率为( )
从1,2,3,4,5,6,7,8中随机取出一个数为x,执行如图所示的程序框图,则输出的x不小于40的概率为( )| A. | $\frac{3}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{1}{2}$ |
6.抛物线y2=4x上的点P到抛物线的准线的距离为d1,到直线3x-4y+9=0的距离为d2,则d1+d2的最小值为( )
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{6}{5}$ | C. | 2 | D. | $\frac{12}{5}$ |
10.长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=1,则异面直线BC1与CD1所成角的余弦值为( )
| A. | $\frac{{\sqrt{10}}}{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{{\sqrt{10}}}{10}$ | D. | $\frac{1}{2}$ |