题目内容
已知角α的顶点在原点,始边与x轴的正半轴重合,终边经过点P(-3, ).
).
(1)求sin 2α-tan α的值;
(2)若函数f(x)=cos(x-α)cos α-sin(x-α)sin α,求函数y= f(
f( -2x)-2f2(x)在区间[0,
-2x)-2f2(x)在区间[0,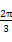 ]上的值域.
]上的值域.
解:(1)因为角α终边经过点P(-3, ),
),
所以sin α= ,cos α=-
,cos α=- ,tan α=-
,tan α=- .
.
∴sin 2α-tan α=2sin αcos α-tan α=- +
+ =-
=- .
.
(2)∵f(x)=cos(x-α)cos α-sin(x-α)sin α=cos x,x∈R,
∴y= cos(
cos( -2x)-2cos2x=
-2x)-2cos2x= sin 2x-1-cos 2x=2sin(2x-
sin 2x-1-cos 2x=2sin(2x- )-1.
)-1.
∵0≤x≤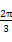 ,∴0≤2x≤
,∴0≤2x≤ ,∴-
,∴- ≤2x-
≤2x- ≤
≤ ,
,
∴- ≤sin(2x-
≤sin(2x- )≤1,∴-2≤2sin(2x-
)≤1,∴-2≤2sin(2x- )-1≤1,
)-1≤1,
故函数y= f(
f( -2x)-2f2(x)在区间[0,
-2x)-2f2(x)在区间[0,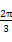 ]上的值域是[-2,1].
]上的值域是[-2,1].

练习册系列答案
相关题目
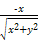 ;③若sin α=sin β,则α与β的终边相同;④第二象限角大于第一象限角.
;③若sin α=sin β,则α与β的终边相同;④第二象限角大于第一象限角.

 (0<α<
(0<α< ,
, )
) ) (D)(
) (D)(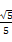 .
. -2α)的值.
-2α)的值.
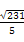 (B)
(B)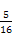 (C)
(C)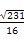 (D)
(D)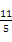
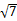 .
.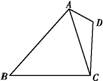
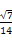 ,sin ∠CBA=
,sin ∠CBA=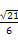 ,求BC的长.
,求BC的长.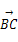 =a,
=a,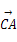 =b,给出下列命题:①
=b,给出下列命题:①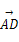 =
= a-b;②
a-b;②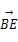 =a+
=a+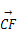 =-
=- =
= ,
, =
= ,
, =
= .
.